Zeitsparend messen mit preisgünstigen Oszilloskopen
Fortsetzung des Artikels von Teil 2
Zeitsparend messen mit preisgünstigen Oszilloskopen
Erweiterte Analysefunktionen: Speichernutzung und Sequenzmodus
Auch in einem einfachen Oszilloskop ist die optimale Speichernutzung ein Thema, denn die verfügbare Signalspeicherkapazität beeinflusst die maximale Messzeit. Denn wenn man die Reaktion eines Messobjekts über eine längere Zeit aufzeichnen kann, hat man mit mehr Speicher mehr Informationen darüber, was in einem Messsignal passiert, und somit eine Basis für eine tiefer gehende Analyse. Die verfügbare Speicherkapazität beeinflusst weiterhin die Abtastrate eines Oszilloskops. Oft wird angenommen, die maximale Abtastrate eines Oszilloskops würde für jede beliebige Einstellung der Horizontalablenkung gelten. Das stimmt so aber nicht: Weil ein Oszilloskop nur eine begrenzte Speicherkapazität hat, muss die Abtastrate sinken, wenn die Messzeit zunimmt. Je größer der Speicher eines Oszilloskops ist, desto länger kann es bei maximaler Abtastrate aufzeichnen. Wie viel Speicherkapazität man braucht, hängt also davon ab, wie lange man bei maximaler Abtastrate messen will. Weil man mit mehr Speicher in allen Einstellungen der Horizontalablenkung eine höhere Abtastrate aufrechterhalten kann, schützt mehr Speicher gegen Aliasing (Faltungseffekt, wenn das Messsignal Frequenzen enthält, die größer als die halbe Abtastfrequenz sind) und liefert mehr Details des Messsignals.
Jobangebote+ passend zum Thema
Bei der Analyse kann es viel Zeit sparen helfen, wenn ein Oszilloskop auf das Messsignal mathematische Operationen anwenden kann. Sie verschaffen dem Anwender einen besseren Einblick in sein Messobjekt. Auf die erfassten Messkurven kann man Addition, Subtraktion, Multiplikation, Division, Integration und Differentiation anwenden und die Ergebnisse dann auf dem Bildschirm anzeigen.
Im Labor bieten mathematische Funktionen Schülern und Studenten eine einzigartige Möglichkeit, praktisch zu lernen. Ein Oszilloskop kann mathematische Zusammenhänge in Echtzeit und real in der Wirklichkeit zeigen. Das ermöglicht es den Ausbildungsstätten für Mathematik, Physik und Ingenieurwesen, „echte“ Anwendungen von Mathematik in einem System zu demonstrieren. Wenn ein Signal und eine mathematische Funktion einmal auf dem Bildschirm dargestellt sind, können die Studenten die Parameter des Signals verändern – etwa die Amplitude, einen Gleichspannungsoffset oder andere Parameter – und unmittelbar die Auswirkungen dieser Veränderungen sehen.
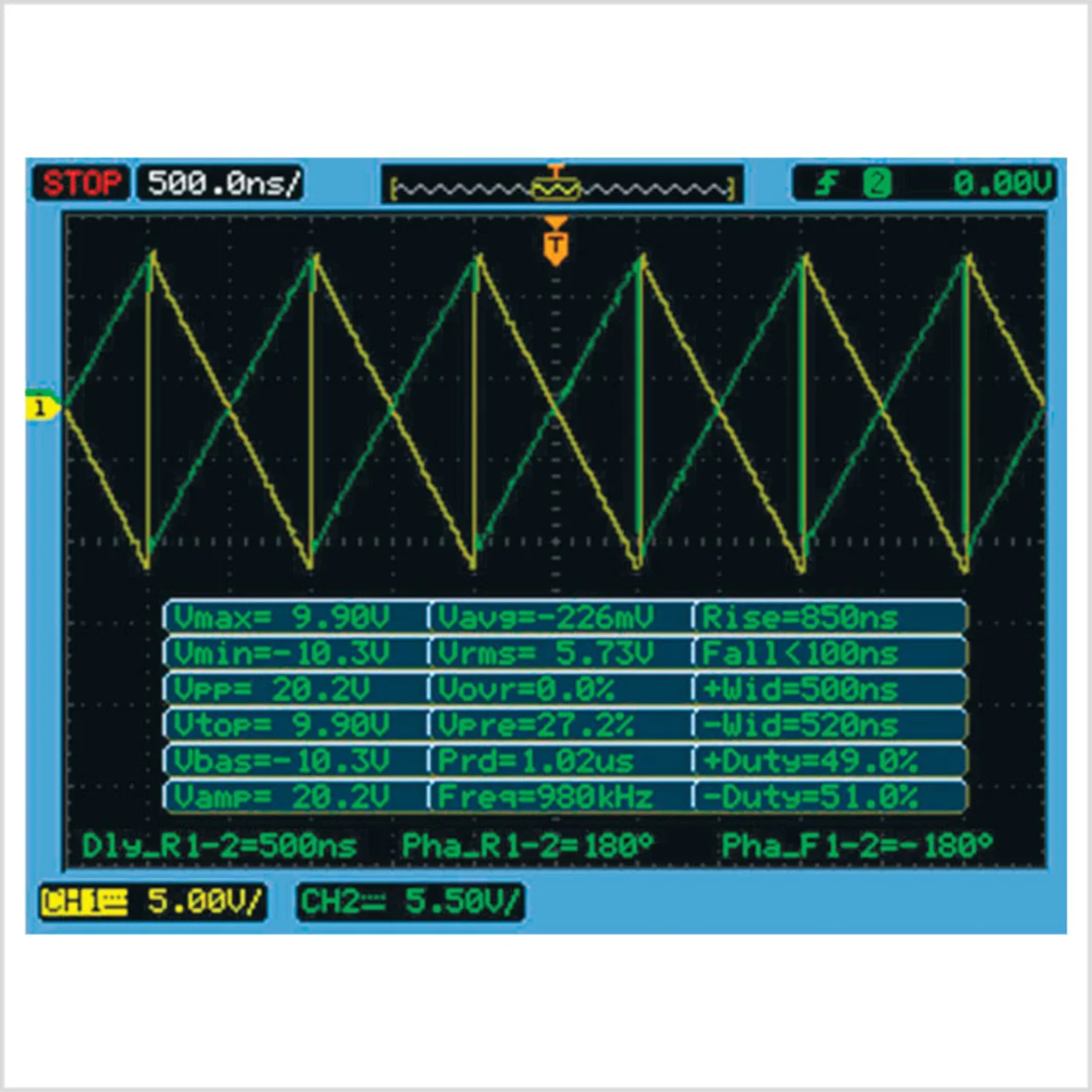
Diese Anschaulichkeit ist didaktisch ausgesprochen wertvoll, wenn Design-Prinzipien und Auswirkungen elektrischer Signaländerungen in einem System gelehrt werden.
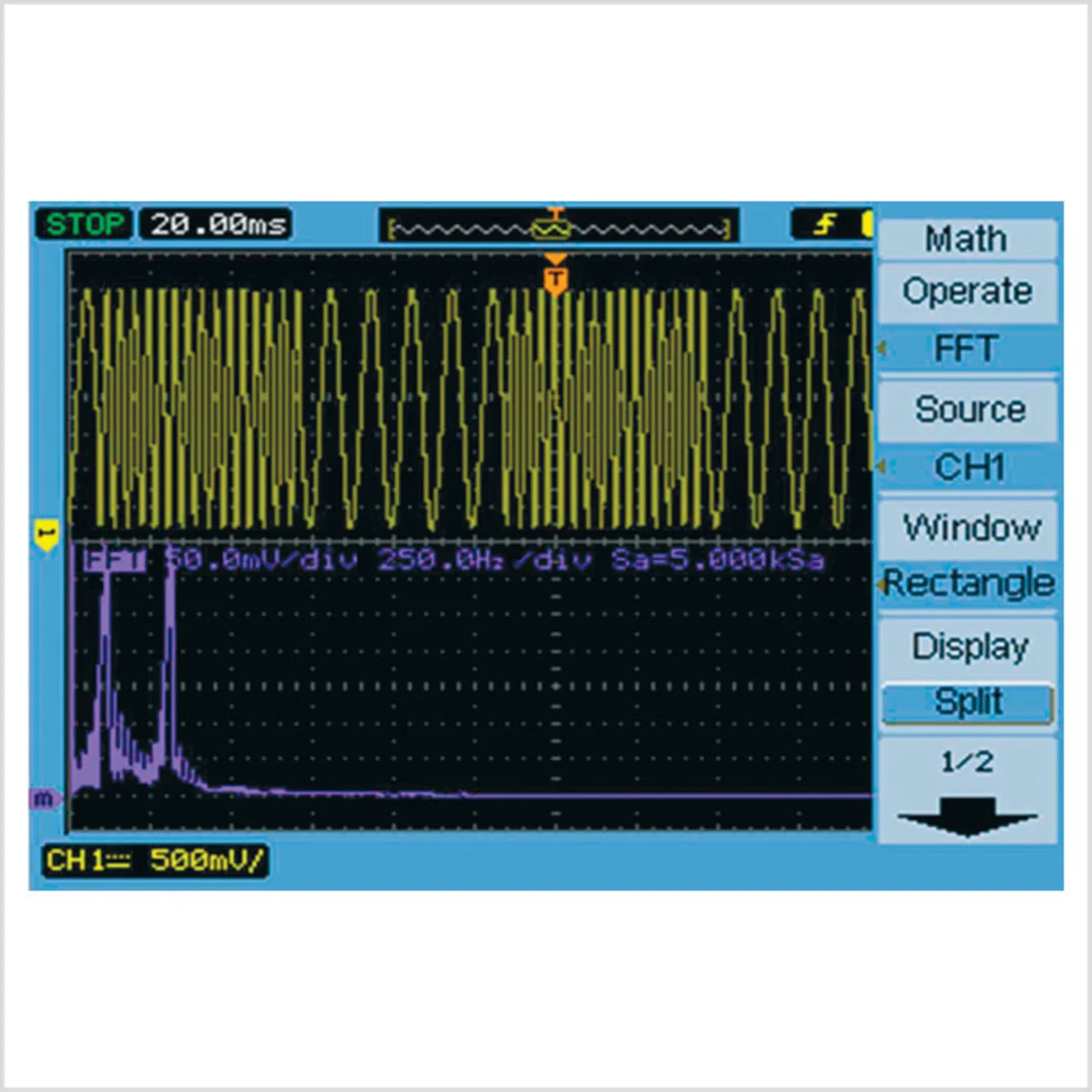
Dass man bereits mit einfachen Oszilloskopen eine FFT-Analyse durchführen kann, ist besonders hilfreich, weil nichtlineare Bauelemente wie z.B. Verstärker in der Elektronik ja sehr weit verbreitet sind. Die durch diese Bauelemente verursachten nichtlinearen Verzerrungen sind letztlich ein häufiges Problem, mit dem jeder Entwicklungsingenieur konfrontiert ist. Um sie zu messen und z.B. Prototypen zu charakterisieren, führt man dem Eingang des Verstärkers ein spektralreines Sinussignal zu und schaut sich dann das Signal am Ausgang mit dem Oszilloskop an. Mittels einer FFT ergibt sich ein Spektrum des Ausgangssignals (Bild 3).
Erweiterte Analysefunktionen: Beispiel Maskentest
Ein Oszilloskop sollte nicht nur eine genaue Signaldarstellung liefern, sondern dazu Analysefunktionen bereitstellen, die das Testen und Verstehen des Designs vereinfachen und beschleunigen. Eine dieser Analysefunktionen auf einfachen Oszilloskopen ist der Maskentest, der besonders in der Produktion und im Qualitätstest nützlich ist.
- Zeitsparend messen mit preisgünstigen Oszilloskopen
- Zeitsparend messen mit preisgünstigen Oszilloskopen
- Zeitsparend messen mit preisgünstigen Oszilloskopen
- Zeitsparend messen mit preisgünstigen Oszilloskopen