Hochintegrierte Mobilfunkempfänger arbeiten mit komplexen Filtern
Höhere Integration mit niedrigerer Zwischenfrequenz
Fortsetzung des Artikels von Teil 2
Komplexe Filter
Die Filterung von komplexen Signalen soll im folgenden genauer analysiert werden. Die Übertragungsfunktion H(jω) eines komplexen Filters setzt sich aus einem Realteil Hr(jω) und einem Imaginärteil Hi(jω) zusammen, so dass gilt:
H(jω) = Hr(jω) + jHi(jω)
Jobangebote+ passend zum Thema
H(jω) lässt sich mit Hilfe von rationalen Polynomfunktionen in jω beschreiben, wobei die Koeffizienten komplex sein können. Wenn X(jω) das Eingangssignal im Frequenzbereich ist, so gilt für das Ausgangssignal Y(jω) des Filters:
Y(jω) = H(jω) · X(jω)
Daraus ergeben sich folgende Beziehungen:
Yr(jω) = Hr(jω) · Xr(jω) – Hi(jω) · Xi(jω)
Yi(jjω) = Hi(jω) · Xr(jω) + Hr(jω) · Xi(jω)
Dabei stellen Xr(jω) und Yr(jω) bzw. Xi(jω) und Yi(jω) jeweils die Real- und Imaginärteile von Ein- und Ausgangssignal dar. Bild 4 zeigt die Umsetzung dieser Beziehungen in ein Blockschaltbild für das komplexe Filter [1, 2, 7]. Eine konkrete Realisierung ist entsprechend diesem Blockdiagramm sowohl in Analog- als auch in Digitaltechnik möglich.

Wie schon angesprochen, sollen die komplexen Filter zur Unterdrückung von positiven oder negativen Frequenzkomponenten von komplexen oder reellen Signalen eingesetzt werden. Dieses Verhalten lässt sich mit Hilfe eines Bandpasses realisieren, dessen Übertragungsfunktion sich durch eine Lineartransformation aus der eines Tiefpasses ergibt. Diese Transformation entspricht einer Verschiebung der Übertragungsfunktion auf der Frequenz-achse und ist wie folgt definiert:

Entsprechend gilt im Digitalbereich, wo die Übertragungsfunktion mit Hilfe der Variablen z = ejωT beschrieben wird, mit der Abtastperiode T:

Durch diese Frequenztransformation werden die Koeffizienten der Polynomfunktion komplex, sodass eine Realisierung nur mit einem komplexen Filter möglich ist. Bild 5 zeigt die Verschiebung der Filterfunktion durch diese Frequenztransformation. Es wird deutlich, dass negative Frequenzanteile unterdrückt werden. Eine physikalische Realisierung ist z.B. mit der Struktur in Bild 4 möglich, wobei allerdings vier Übertragungsfunktionen implementiert werden müssen.
Betrachtet man als Beispiel ein analoges Tiefpassfilter erster Ordnung, so führt die lineare Frequenztransformation zu einem komplexen Bandpass zweiter Ordnung, dessen Übertragungsfunktion sich in einen Realteil und einen Imaginärteil jeweils zweiter Ordnung aufspalten lässt. Es gelten folgende Beziehungen:


Entsprechend Bild 4 müssen also 2 x 2 Filterübertragungsfunktionen zweiter Ordnung realisiert werden. Im Vergleich dazu sind für die Filterung des komplexen Signals durch ein reelles Bandpassfilter nur zwei Übertragungsfunktionen zweiter Ordnung erforderlich. Dieses Filter würde zwar in etwa die gleiche Sperrdämpfung erzeugen, aber zwei Durchlassbereiche aufweisen, einen bei positiven und einen bei negativen Frequenzen.
Um den Realisierungsaufwand für komplexe analoge Filter zu reduzieren, wurde von Voormann [2, 7] eine direkte Synthesemethode entwickelt, bei der nur zwei Übertragungsfunktionen erster Ordnung realisiert werden müssen. Die Übertragungsfunktion des Bandpassfilters wird dazu wie folgt dargestellt:
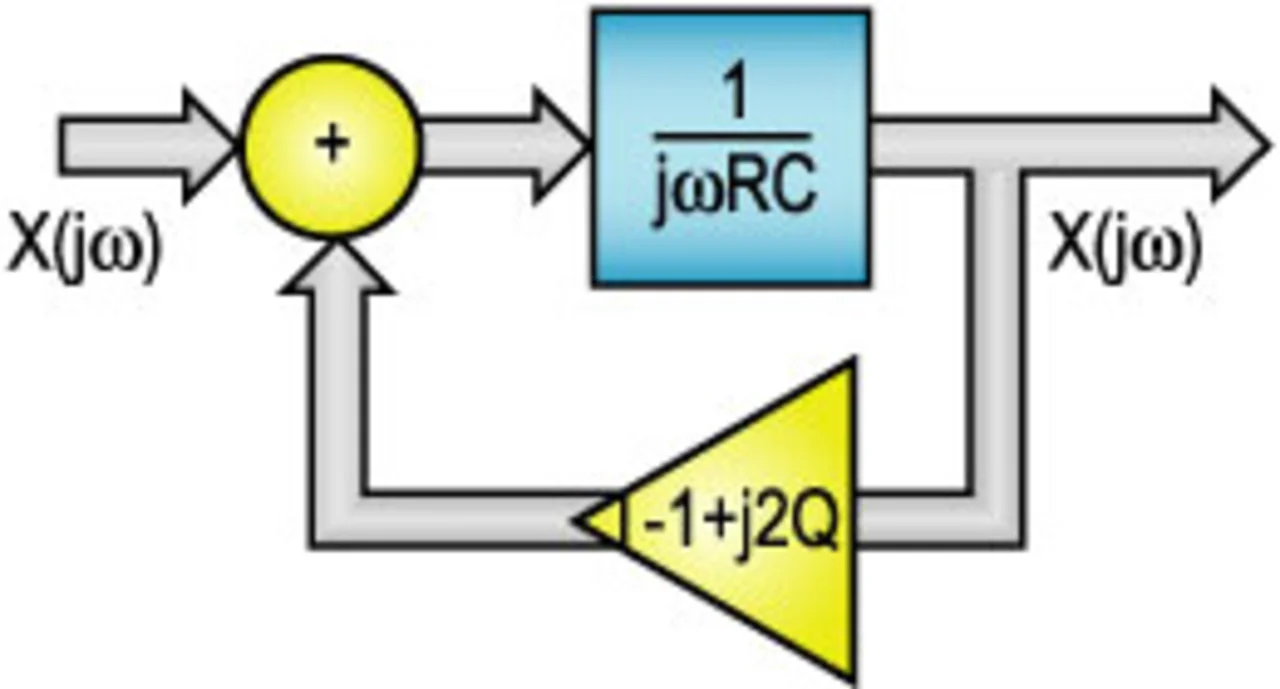

mit Q = ω0/(2ωB). Hierbei ist ωB die Bandbreite des ursprünglichen Tiefpassfilters, 2ωB die Bandbreite des Bandpasses und Q die Filtergüte. Diese Gleichung kann nun wie folgt umgestellt werden:

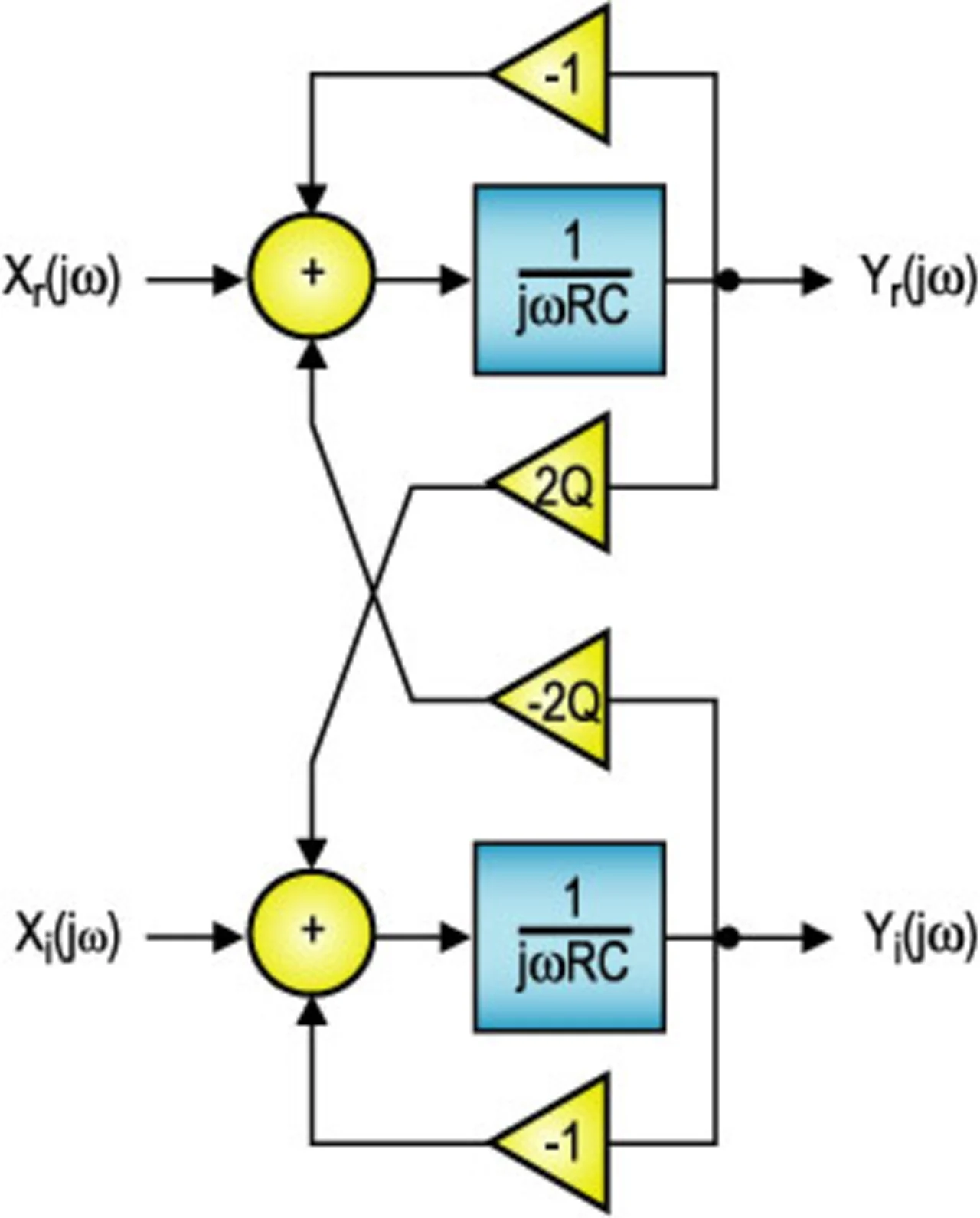
Mit Hilfe dieser Beziehung lässt sich das Filter direkt synthetisieren. Bild 6 zeigt das entsprechende Blockdiagramm mit den komplexen Größen, es wird lediglich ein Integrator und ein komplexer Verstärker benötigt. Die Realisierung mit reellen Signalen ist in Bild 7 zu sehen. Xr(jω) und Xi(jω) repräsentieren den Real- und Imaginärteil des Eingangssignals, während Yr(jω) und Yi(jω) die entsprechenden Komponenten des Ausgangssignals darstellen. Die Unterdrückung des unerwünschten Seitenbandes wird in erster Linie durch die Genauigkeit und die Matching-Eigenschaften der Filterkomponenten bestimmt.
Filter höherer Ordnung lassen sich sehr einfach durch Kaskadierung dieses Filterblocks realisieren. Für einen Bandpass 10. Ordnung, der sich durch Frequenztransformation aus einem Tiefpass 5. Ordnung ergibt, werden zehn Operationsverstärker benötigt. Dieser Filtertyp wird auch als „Active integrated sequence asymmetric Polyphase Filter“ [1] bezeichnet und wird bevorzugt für niedrigere Frequenzbereiche eingesetzt, z.B. in einem Low-IF-Empfänger nach der Umsetzung auf die ZF.
Integrierte Bausteine mit Low-IF-Empfängerarchitektur
Auf Tagungen und in wissenschaftlichen Zeitschriften wurde in den letzten Jahren eine Reihe von Testchips und Prototypen mit einer Low-IF-Architektur vorgestellt, die für verschiedene Mobilfunkanwendungen entwickelt worden sind [3, 6, 8, 9]. Das Low-IF-Konzept hat sich aber inzwischen auch in kommerziellen Produkten als Empfängerarchitektur bei Bausteinen gemäß der Standards GSM, DECT und Bluetooth etabliert [10, 11]. Im Folgenden werden einige verfügbare Bausteine genauer beschrieben. Die Aufstellung erhebt allerdings in keiner Weise den Anspruch auf Vollständigkeit.
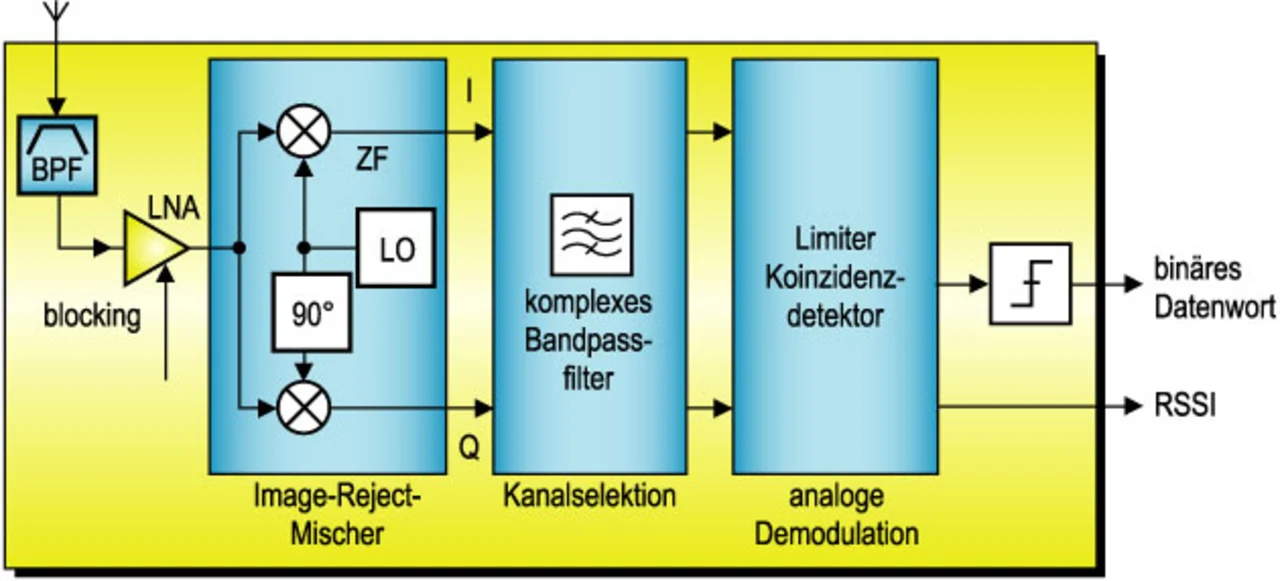
Der amerikanische IC-Hersteller National Semiconductor (www.national.com) bietet ein Chip-Set für das DECT-Band bei 1,9 GHz an, das aus einem Basisbandbaustein, der in unterschiedlichen Varianten verfügbar ist, sowie dem Transceiverbaustein LMX 4168 besteht. Dieser basiert in Empfangsrichtung auf einer Low-IF-Architektur, wie sie in Bild 8 dargestellt ist. Die ZF liegt bei 864 kHz, was dem halben Kanalabstand von DECT entspricht. Bei dieser niedrigen ZF erfolgt die Kanalselektion durch ein analoges komplexes Bandpassfilter (Polyphasenfilter). Zusätzlich sind in Empfangsrichtung weitere analoge Signalverarbeitungsblöcke integriert. Hierzu gehören insbesondere ein LNA (Low Noise Amplifier), der Quadraturmischer und die Demodulation. Der Baustein wird in CMOS-Technologie gefertigt und ist in einem platzsparenden 48-Pin-Gehäuse untergebracht. Zusätzlich muss aus dem analogen Signal nach der Kanalfilterung noch die Information über die Empfangsfeldstärke bestimmt werden (RSSI: Radio Signal Strength Indication). Dieses ist z.B. mit Hilfe eines Limiterverstärkers möglich, der auch im Demodulator eingesetzt werden kann.
Ähnliche Bausteine werden von den europäischen IC-Herstellern Infineon (www.infineon.com) und Philips (www.philips.com) angeboten. Der PMB 6610 von Infineon wird in BiCMOS-Technologie gefertigt. Der UAA3545 von Philips, ebenfalls ein BiCMOS-Baustein, ist in einem sehr kleinen LQFP-32-Gehäuse mit den Abmessungen 5 x 5 mm2 untergebracht. Beide Bausteine realisieren die Demodulation in Analogtechnik mit Hilfe eines Limiterverstärkers und eines Koinzidenzdemodulators. Für die Digitalisierung wird daher nur ein einfacher Komparator benötigt, wie Bild 8 zeigt.
Da Bluetooth sehr viele Gemeinsamkeiten mit DECT aufweist – es wird z.B. GFSK (Gaussian Frequency Shift Keying) als Modulationsverfahren eingesetzt und ein TDMA-Verfahren verwendet –, war es für die IC-Hersteller naheliegend, ihre DECT-Bausteine für Bluetooth weiterzuentwickeln. Alle drei Unternehmen bieten daher auch eine hochintegrierte Bluetooth-Lösung basierend auf dem Low-IF-Konzept an. Darüber hinaus setzen mittlerweile alle Hersteller auch für die HF-Funktionen eine Standard-CMOS-Technologie ein, sodass auch eine Komplettlösung auf einem IC realisierbar ist. Unter anderem bietet Infineon mit seinen BlueMoon-Bausteinen PMB 876x eine solche Ein-Chip-Bluetooth-Lösung an, die in einer 0,13-µm-Technologie gefertigt wird. Die Gehäuseabmessungen der ICs konnten bei den neuesten Varianten auf nur noch 5 x 5 mm2 reduziert werden.
Auch der britische Hersteller CSR (www.csr.com) dessen Bluetooth-Module einen großen Kundenkreis gefunden haben, setzt auf eine Low-IF-Architektur. Bei der neuesten Variante der Ein-Chip-Lösung, dem BlueCore 3, erfolgt die Demodulation durch einen digitalen FSK-Diskriminator, um eine bessere Performance als bei den analogen Lösungen zu erreichen. Darüber hinaus werden von verschiedenen Herstellern Transceiver-Bausteine für Anwendungen im ISM-Band bei 2,4 GHz angeboten, die ebenfalls eine Low-IF-Architektur für den Empfangspfad haben.
- Höhere Integration mit niedrigerer Zwischenfrequenz
- Neue Architekturkonzepte für integrierte Empfänger
- Komplexe Filter