Algorithmus auf ARM
ARM-Befehlssätze im Vergleich
Fortsetzung des Artikels von Teil 1
Wollen Sie mehr wissen?
Mehr spannende Informationen rund um ARM-Architekturen gibt es beim großen DESIGN&ELEKTRONIK-Entwicklerforum »ARM erfolgreich einsetzen« am 10. Oktober 2007 in München. Erfahren Sie alles über die neuesten Entwicklungen, treffen Sie erfahrene Experten und ziehen Sie Gewinn aus den hochkarätigen Vorträgen. Details finden Sie unter www.elektroniknet.de/home/termine/arm2007/arm-erfolgreicheinsetzen-2007/
Jobangebote+ passend zum Thema
Literatur:
[1] Taschenbuch der Mathematik, 6. Auflage, I.N. Bronstein, Verlag Harri Deutsch, ISBN 3-8171-2006-0
[2] User’s Manual for Keil Compiler, V1.2, November 2003
[3] html?/access//helpdesk/help/toolbox/fixpoint/ug/glossary.html#f8006>www.mathworks.com
[4] ARM Developer Suite, Version 1.2, Assembler Guide, 2001 ARM Limited
Autoren:
Prof. Dr.-Ing. Klaus-Dietrich Kramer ist Projektleiter,
Thomas Banse ist wissenschaftlicher Mitarbeiter des Mikrocontroller-Applikationszentrums an der Hochschule Harz MCAC.
Hochschule Harz MCAC
Telefon 0 39 43/65 93 17
www.mcac-hs-harz.de
verwandter Artikel:
Einstieg in die ARM-Welt
Der Algorithmus wurde in der IDE »µVision 3« von Keil zunächst in C-Code umgesetzt. Hierbei gelten folgende Datentypen per Definition als Vereinbarung: »Byte«: 8 Bit vorzeichenbehaftet für Q0.7, »Word«: 16 Bit vorzeichenbehaftet für Q0.15, »dWord«: 32 Bit vorzeichenbehaftet für Q0.31, »Float«: 32 Bit nach IEEE.
Die C-Routine für Q0.15 stehe beispielhaft für die drei betrachteten Festkommaformate (Kasten »C-Code«). Die nachfolgenden Routinen arbeiten alle nach dem gleichen Algorithmus, der eine aufgerollte Programmstruktur nutzt (ohne Schleifendurchlauf).
Die Laufzeitmessung ergibt bei einem Core-Takt von 60 MHz die folgenden Zeiten: Float: 83,7 µs, signed Q0.7: 9,1 µs, signed Q0.15: 9,9 µs, signed Q0.31: 24,9 µs. Der C-Compiler arbeitet dabei mit der höchsten Optimierungsstufe hinsichtlich Laufzeit.
Als nächster Schritt findet die Handoptimierung für das Festkommaformat auf Assemblerebene statt, wobei der gleiche Programmablauf verwendet wird. Bei den Formaten Q0.7 und Q0.15 greifen die Befehle des ARM-Befehlssatzes mit dem flexiblen zweiten Operanden besonders. Durch diesen zweiten Operanten lässt sich beispielsweise die Addition eines Koeffizienten zusammen mit der Kommastellenkorrektur und dem Runden aus der vorherigen Multiplikation in einem Befehl ausführen (Beispiel: »add r2,r4,r2,asr #15«). Beim Q0.31-Format spielt die 64-Bit-Multiplikation ihre Stärke aus. Die Laufzeitmessung ergibt die folgenden Zeiten: signed Q0.7: 8,8 µs, signed Q0.15: 9,7 µs, signed Q0.31: 16,2 µs.
Als nächstes steht die Implementierung des Algorithmus’ im Thumb-Befehlssatz an. Hierfür wurde der C- und Assembler-Code auf Thumb umgeschrieben. Bei identischen Testbedingungen ergeben sich für die Laufzeiten der C-Routinen folgende Werte: 90,0 µs für Float, 11,5 µs für signed Q0.7, 12,7 µs für signed Q0.15 und 51,3 µs für signed Q0.31.

Der Vergleich mit den Assemblerroutinen beschränkt sich auf das Q0.15-Format, da hier eine ausreichende Genauigkeit zur Verfügung steht. In Assembler ergibt sich eine Laufzeit von 12,2 µs für dieses Format.
Bezüglich der Laufzeitunterschiede zwischen dem ARMund dem Thumb-Befehlssatz ergibt sich ein Vorteil für den ARM-Befehlssatz. Dieser benötigt rund 20% weniger Ausführungszeit für den Algorithmus. Der Thumb-Befehlssatz hat jedoch einen anderen Vorteil: Ein Thumb-Befehl benötigt nur eine halbe Befehlslänge (16 Bit) gegenüber dem ARM-Modus (32 Bit). Die Codegröße ist beispielsweise für das Q0.15-Format im Thumb-Modus um etwa 22% kleiner als im ARM-Modus. Die Laufzeitvorteile gegenüber dem Fließkommaformat sprechen deutlich für den Einsatz eines Qn.m-Formats. Der ARM-Befehlssatz bringt hierfür leistungsstarke Befehle mit. Zudem ist beim Q0.15-Format quasi kein Genauigkeitsunterschied gegenüber Fließkomma mehr vorhanden. Eine gründliche Betrachtung des Zahlenvorrates und des Overflows sei vorweggenommen. Kommt es zudem auf jedes Byte im Speicher an, so stellt der Thumb-Befehlssatz ohne zusätzliche Fließkommabibliothek beziehungsweise deren Makros eine weitere Alternative dar.

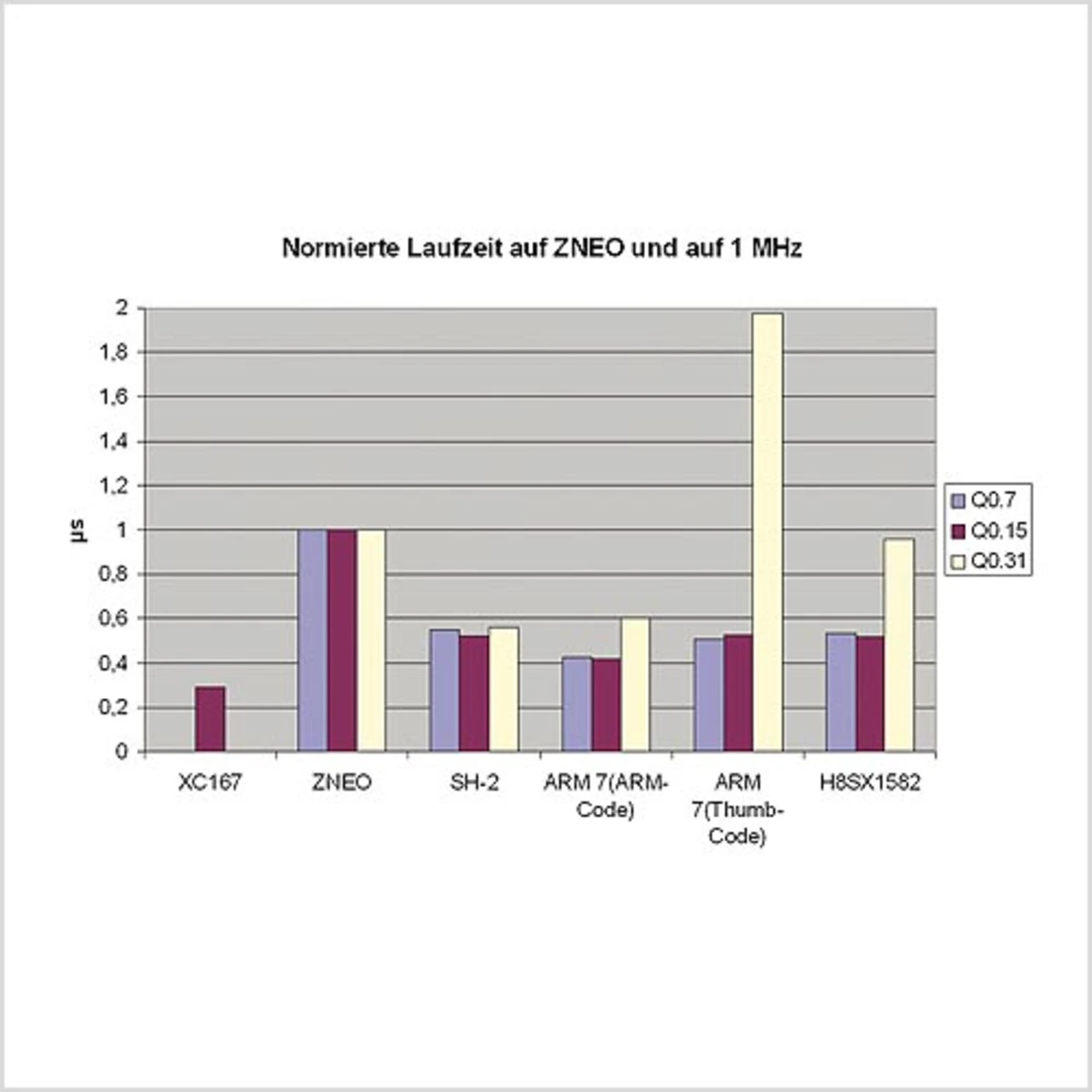
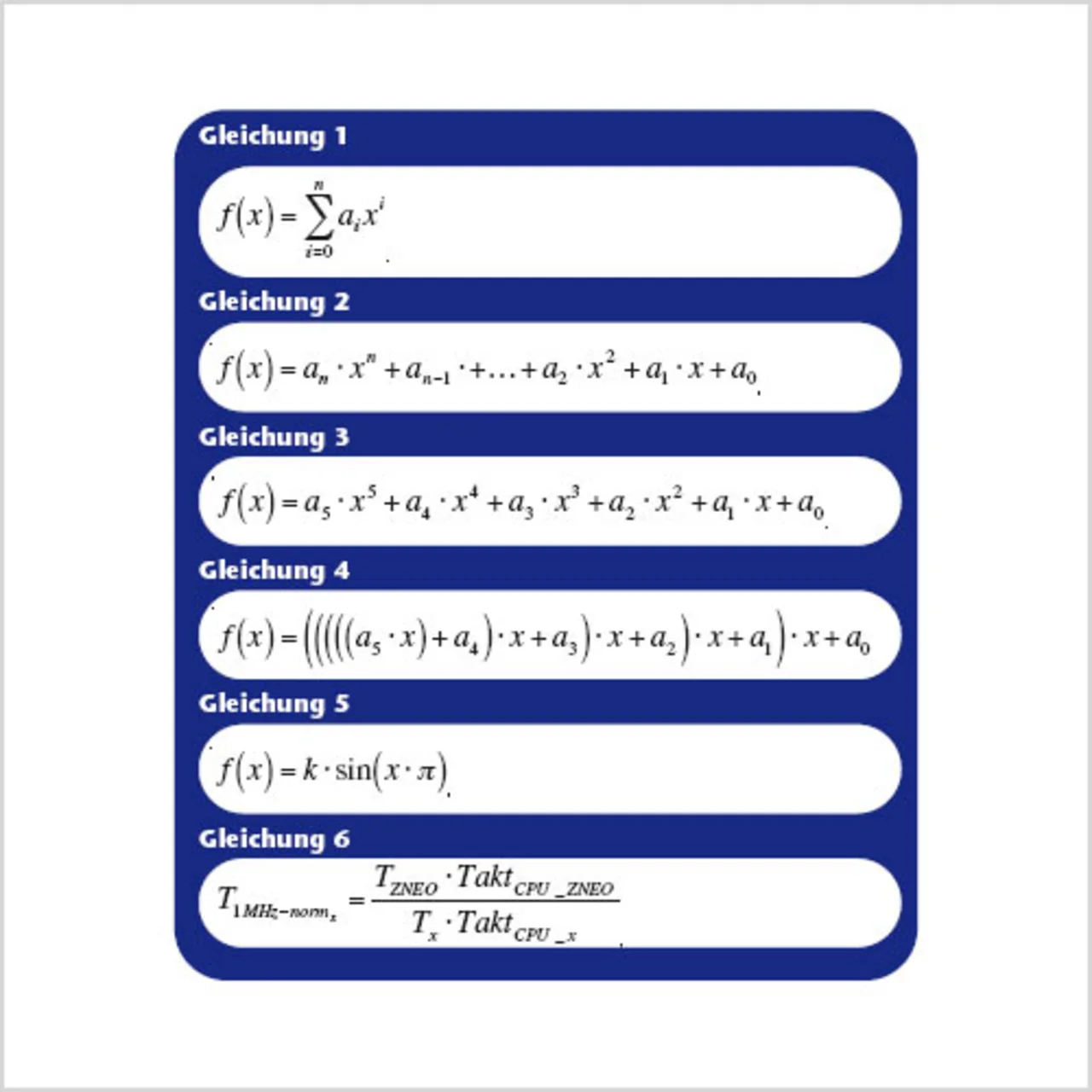
Der genannte Algorithmus wurde in weiteren Systemen implementiert. Die Ergebnisse der Laufzeituntersuchungen mit dem Qn.m-Format sind in Bild 3 dargestellt. Das beschriebene Beispiel dient hierbei als Benchmark. Das Diagramm zeigt nach Gleichung (6) die Laufzeit, normiert auf den ZNEO der Firma Zilog und auf einen einheitlichen CPU-Takt von 1 MHz. Durch diese Normierung kann man direkt die unterschiedlichen Architekturen miteinander vergleichen. Tx ist die Laufzeit des jeweiligen Testsystems, TaktCPU_x ist der Takt der Test-CPU.
In den bisherigen Ergebnissen schneidet der »XC167« von Infineon aufgrund seiner speziellen DSP-Hardware am Besten ab. Diese MCU ist auf das signed Q0.15- bzw. auf das unsigned Q1.15-Format optimiert, für welches eine leistungsstarke Bibliothek zur Verfügung steht. Der ARM7 liegt bei den konventionellen MCUs ohne spezielle Beschleunigerhardware vorn. Das Projekt Mikrocontroller-Applikationszentrum (MCAC) wird im Rahmen des Kompetenznetzwerks für angewandte Transferorientierte Forschung (KAT) durch das Land Sachsen-Anhalt gefördert.

Um die Performance des Algorithmus gegenüber einer Fließkommalösung zu erhöhen, kommt für die Berechnung das Festkommaformat »Qn.m« zum Einsatz. Bei diesem Zahlenformat steht »n« für die Vorkommastellen (Anzahl Bits) und »m« für die Nachkommastellen (Anzahl Bits). Eine Unterscheidung in signed und unsigned wird, wie gewohnt, über das MSB (Most Significant Bit) vorgenommen. So ist beispielsweise »unsigned Q16.0« eine gewöhnliche vorzeichenlose 16-Bit-Zahl. »signed Q0.15« ist eine 16-Bit-Zahl wobei hier das MSB das Signum dargestellt und damit der Bereich -1 <= x <= 1-2-15 abgebildet wird. Das Vorzeichen ist zudem als erste Vorkommastelle zu deuten, geht jedoch in n nicht mit ein.
Für die Gegenüberstellung werden die Formate »signed Q0.31«, »signed Q0.15« und »signed Q0.7« umgesetzt. Im Folgenden werde jegliche Qn.m-Bezeichnung als vorzeichenbehaftet gedeutet. Da die meisten Compiler dieses Zahlenformat nicht unterstützen, ist es sinnvoll, die beiden Grundrechenoperationen, welche für die Berechnung in Frage kommen, näher zu betrachten. Bei der Addition zweier gleich skalierter Qn.m-Zahlen (etwa zwei Q0.15-Zahlen) findet die normale Addition Verwendung. Bei der Multiplikation gilt es, mehr zu beachten. Die Multiplikation ist vorzeichenbehaftet, und wie im dezimalen System ist die Kommastellenkorrektur zu beachten. Dies geschieht in Abhängigkeit von »n« der beiden Multiplikatoren durch einen einfachen oder mehrfachen Schiebebefehl nach links. Weiterhin wird bei der Multiplikation noch eine Rundung vorgenommen, sodass das gleiche Zahlenformat als Ergebnis entsteht (vgl. Kasten »Multiplikation zweier Q0.15-Zahlen«).

In Bild 1 ist die Sinusfunktion mit jeweils einem der drei Festkommavarianten zusammen gezeigt. Die behandelten Formate sind das Q0.7 (Bild1, oben), Q0.15 (Bild 1, Mitte) und das Q0.31 (Bild 1, unten). Um einen Overflow während der Berechnung zu verhindern, wurde der Sinus wie in Gleichung (5) normiert. Die maximale Abweichung vom echten Sinus aus (5) beträgt im Intervall -0,5 <= x <= 0,5 für Q0.7 5,5%, für Q0.15 0,23% und für Q0.31 ebenfalls 0,23%, jeweils auf die doppelte Amplitude bezogen. Dies zeigt, dass das Q0.15-Format eine ausreichende Genauigkeit, auch gegenüber dem Floating-Point-Format, erzielt.
Der Algorithmus wurde für alle Datenformate auf dem ARM7TDMI (LPC2138) implementiert. Eine Laufzeitmessung erfolgt dabei über jeweils zehn Berechnungen mit unterschiedlichen Eingangswerten. Auf diese Weise lassen sich Laufzeitunterschiede in der Multiplikation bei unterschiedlichen Multiplikatoren berücksichtigen. Die Laufzeitmessung dient dem Datenformatvergleich und dem Systemvergleich. In Bild 2 ist das verwendete ARM7-Entwicklungssystem der Firma Keil dargestellt.
- ARM-Befehlssätze im Vergleich
- Wollen Sie mehr wissen?