Mit Funktionen so einfach rechnen wie mit Variablen

Mit Funktionen so einfach rechnen wie mit Variablen

Dieser Ansatz funktionierte, hatte aber einige Nachteile. Der wichtigste davon ist, dass viele der auszuwertenden Funktionen mehr als ein Argument benötigen. Die gewünschte Maximierung soll jedoch häufig nur für einige dieser Argumente stattfinden, während andere als einfache Parameter behandelt werden sollen.

Aus diesem Grund führte MathWorks die „Function-Handles“ ein. Die mit der Behandlung von Strings verbundenen Benennungsprobleme wurden damit beseitigt. Dem Funktionsnamen wurde einfach ein „@“-Zeichen vorangestellt, beispielsweise @ertrag, wodurch ein Function-Handle entstand, mit dem die Funktion ertrag aufgerufen werden konnte. Dieses Handle ließ sich sowohl an Routinen übergeben als auch von feval aufrufen.

Jobangebote+ passend zum Thema

MACNICA ATD EUROPE - Ihre berufliche Zukunft

MACNICA ATD Europe GmbH, Ingolstadt

---

Alle Jobangebote im Elektroniknet Karrierebereich anzeigen

Anonyme Funktionen

Matlab 7 löst das Problem der „überflüssigen Argumente“ zusätzlich noch auf andere Weise, nämlich durch anonyme Funktionen, die eine Erweiterung der Function-Handles darstellen. Angenommen, ertrag benötigt drei Argumente, soll aber nur über das zweite Argument maximiert werden, während die beiden anderen konstant sind (in diesem Beispiel 1,5 und 2,5). Formuliert wird dies so:

h = @(x) ertrag(1.5, x, 2.5);

Mit dieser Aktion wird das Function-Handle h erzeugt, welches die Funktion ertrag aufruft, sobald es selber zusammen mit einem Argument x aufgerufen wird.

Diese Funktion ist anonym, weil sie – im Gegensatz zu den älteren Function-Handles – keinen eigenen Namen mehr hat. Function-Handles lassen sich ganz direkt und ohne den Umweg über feval aufrufen. Das gezeigte Handle h kann jetzt etwa mit einem Wert von 0,75 aufgerufen werden:

h(.75)

Mithilfe anonymer Funktionen lassen sich Funktionen über beliebige Argumente maximieren, während andere Argumente konstant bleiben können. Es ist nicht nötig, dass die Argumente durchnummeriert oder zusätzlich an die Maximierungsroutine übergeben werden müssen. Ein weiteres Beispiel dafür stellt eine anonyme Funktion dar, die die Summe aus zwei Funktionen bildet:

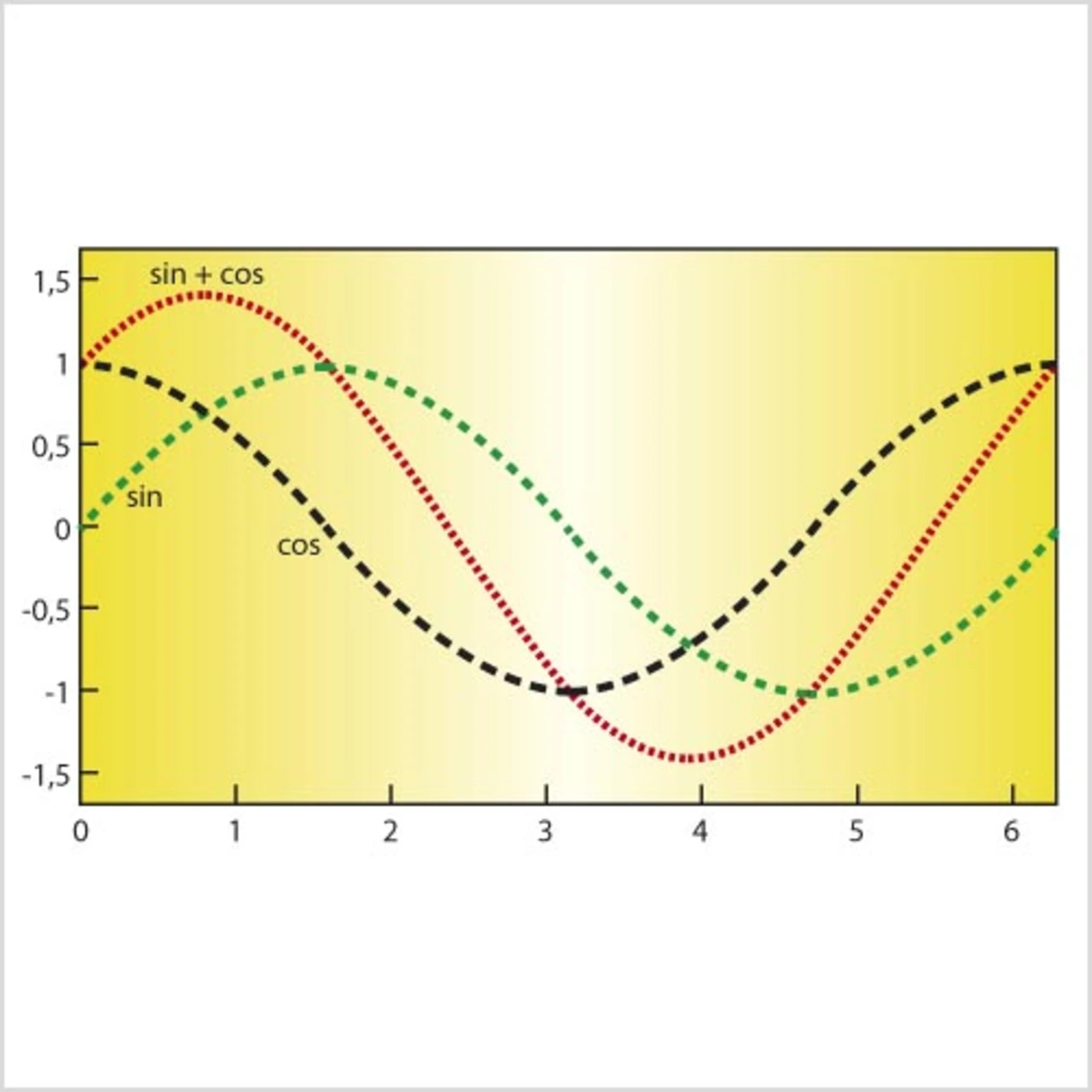
h = @(x)(sin(x)+cos(x));

h ist eine Funktion, die die Summe aus Sinus und Cosinus von x bildet (Bild). Auf dieser Grundlage lässt sich eine erste Version der Funktion fadd erzeugen, die zwei Funktionen (Function-Handles) entgegennimmt und eine neue Funktion als deren Summe ausgibt. Dazu wird die oben gezeigte anonyme Funktion, die zwei Funktionen addiert, in eine weitere anonyme Funktion eingeschlossen, die die benötigten Function-Handles definiert:

fadd = @(f,g)@(x)(f(x)+g(x));

Mit fadd lässt sich das Beispiel aus dem vorigen Abschnitt umformulieren:

h = fadd(@sin, @cos);

Function-Factories

Beim wissenschaftlichen Rechnen bedient man sich häufig so genannter „Function-Factories“. Das sind Funktionen, die ein oder mehrere Function-Handles ausgeben. Ein anschauliches Beispiel einer Function-Factory ist die Interpolation. Angenommen, es sind zwei Vektoren X und Y gegeben. X enthält Punkte auf einer Achse und Y die zu diesen Punkten gehörenden Funktionswerte. In Matlab lässt sich mithilfe der spline-Funktion zwischen diesen Punkten eine stückweise stetige Polynom-Funktion interpolieren:

pp = spline(X, Y);

Das Ergebnis pp enthält die Koeffizienten und Wertebereiche der durch die Interpolation erzeugten Abschnitte. Um den Wert der Interpolation am Punkt x zu ermitteln, muss der Nutzer eine weitere Funktion aufrufen, die von pp und x abhängt:

y = ppval(pp, x);

1. Mit Funktionen so einfach rechnen wie mit Variablen
2. Mit Funktionen so einfach rechnen wie mit Variablen
3. Mit Funktionen so einfach rechnen wie mit Variablen