Reduzierung von Netzoberwellen korrekt berechnen
Die stetige Zunahme nichtlinearer Lasten am Netz beeinträchtigt im hohen Maße die Netzqualität. Dabei spielen die harmonischen Oberwellen eine wesentliche Rolle: Sie sind die Ursache für die Überlastung der Netzinfrastruktur. Zur Reduzierung der Oberwellen dienen passive und aktive Oberwellenfilter. Deren korrekte Bemessung und Auswahl ist Thema dieses Beitrags.
Die stetige Zunahme nichtlinearer Lasten am Netz beeinträchtigt im hohen Maße die Netzqualität. Dabei spielen die harmonischen Oberwellen eine wesentliche Rolle: Sie sind die Ursache für die Überlastung der Netzinfrastruktur. Zur Reduzierung der Oberwellen dienen passive und aktive Oberwellenfilter. Deren korrekte Bemessung und Auswahl ist Thema dieses Beitrags.
Jobangebote+ passend zum Thema
Die Belastung der Netzinfrastruktur durch Oberwellen hat in den vergangenen Jahren markant zugenommen. Oberwellenströme werden durch so genannte nichtlineare Lasten verursacht. Eine nichtlineare Last ist ein elektrischer Verbraucher, der bei sinusförmiger Spannungsversorgung einen nichtsinusförmigen Strom vom Netz bezieht. Diese Oberwellenströme fließen zusätzlich zur „aktiven“ Sinuswelle, sorgen für Zusatzverluste der elektrischen Installationen und können zu thermischer Überlast führen.
Fließen oberwellenbehaftete Ströme durch die Netzimpedanz, so entsteht ein Spannungsabfall, der die Qualität der Netzspannung kompromittiert. Sensitive Verbraucher, z.B. medizinische Geräte oder eine IT-Infrastruktur, können durch die Versorgung mit einer verzerrten Netzspannung in ihrer Funktion beeinträchtigt werden. Zur Erfüllung nationaler und internationaler Normen werden heute auf allen Ebenen der Netzinfrastruktur Maßnahmen zur Oberwellenreduktion getroffen. Dieser Beitrag konzentriert sich auf passive und aktive Oberwellenfilter für Niederspannungsanlagen.
Gängige Topologien nichtlinearer Lasten
Für die weiteren Betrachtungen steht die B6-Gleichrichterbrücke im Mittelpunkt. Dem Dreiphasen-Gleichrichter kommt eine zentrale Bedeutung zu, weil ein Großteil der elektrischen Energie von Verbrauchern mit dieser Eingangsschaltung bezogen wird. Eine typische Anwendung ist der Frequenzumrichter zur Drehzahlregelung von Motoren.
Die gängigsten B6-Gleichrichter-Topologien sind in Bild 1 dargestellt. Topologie A enthält keinerlei magnetische Bauteile zur Stromglättung.
Topologie B wird mit einer vorgeschalteten Induktivität Lac betrieben, üblicherweise einer Netzdrossel (Blechpaket). Topologie C hat eine DC-Drossel Ldc, wie sie in Umrichtern höherer Leistung integriert ist.
Bei allen drei Topologien ist auf der linken Seite das Netz inklusive Netzimpedanz Zline schematisch dargestellt. Rechts repräsentiert die konstante Leistungssenke „P = const“ die von Umrichter und Motor bezogene Wirkleistung, die hier mit 20 kW angenommen wird.
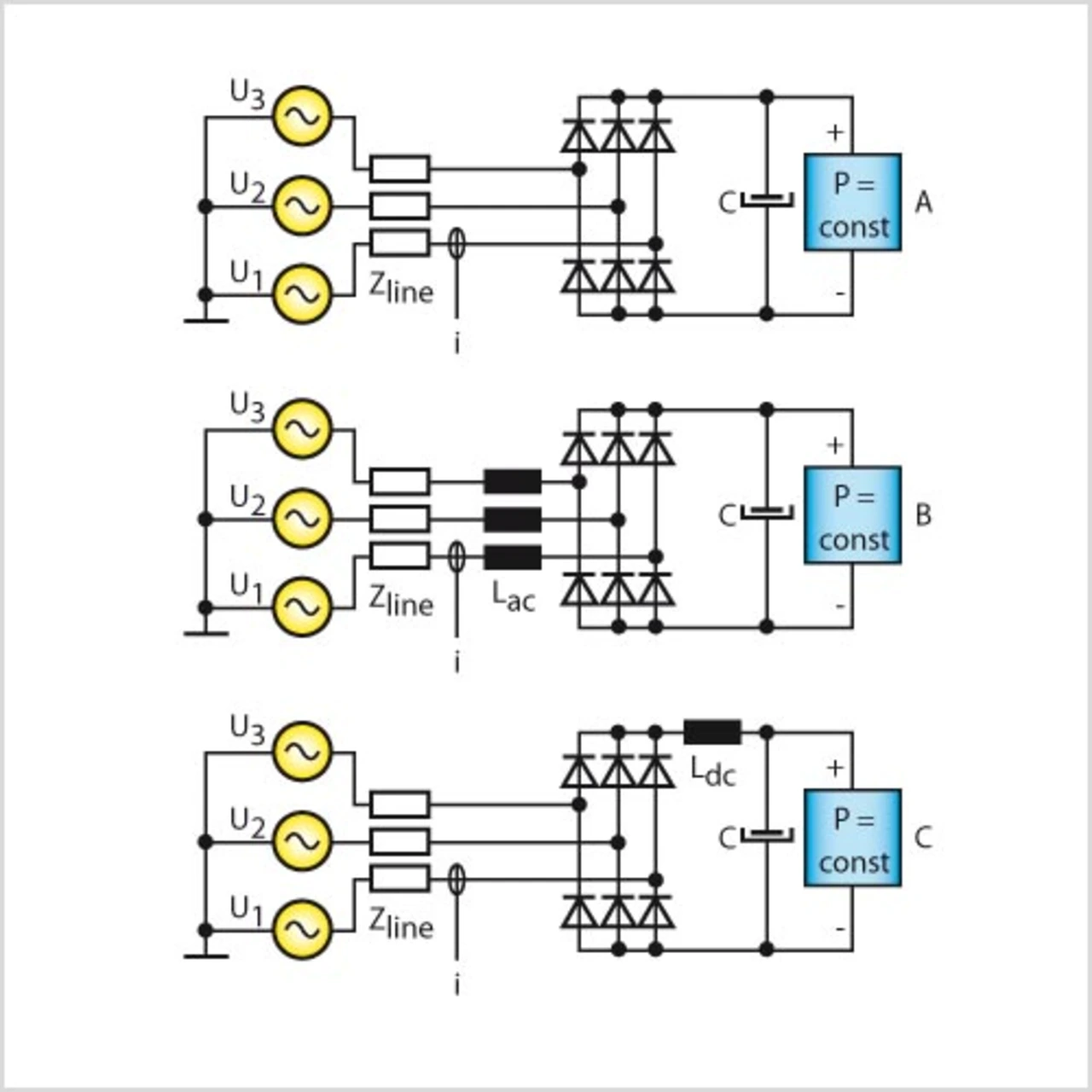
Bild 2 zeigt den Eingangsstrom i für die Topologien A, B und C bei Versorgung durch ein symmetrisches Drehstromnetz. Zline stellt die Ersatzimpedanz dar, bestehend aus Verteiltransformator, Netzleitung, Sicherungen usw., die für dieses Beispiel als halb induktiv und halb ohmsch betrachtet wird (L = 18 μH; R = 6 mΩ). Ferner werden folgende Werte angenommen:
- Zwischenkreiskondensator: C = 2000 μF
- Wechselstrom-Netzdrossel (Topologie B): L<sub>ac</sub> = 500 μH
- Gleichstrom-Zwischenkreisdrossel (Topologie C): Ldc = 1 mH
Die nichtsinusförmigen Ströme i (weiße Kurven aus Bild 2), die von der sinusförmigen Spannungsquelle bezogen werden, lassen sich in zwei orthogonale Anteile, ia (aktiv) und ib (reaktiv) aufteilen:

Der aktive Strom ia (grün), der Wirkstrom, ist eine mit der Spannung phasengleiche sinusförmige Grundschwingung (Bild 3). Dieser Stromanteil ist als einziger an der Übertragung von Wirkleistung beteiligt.
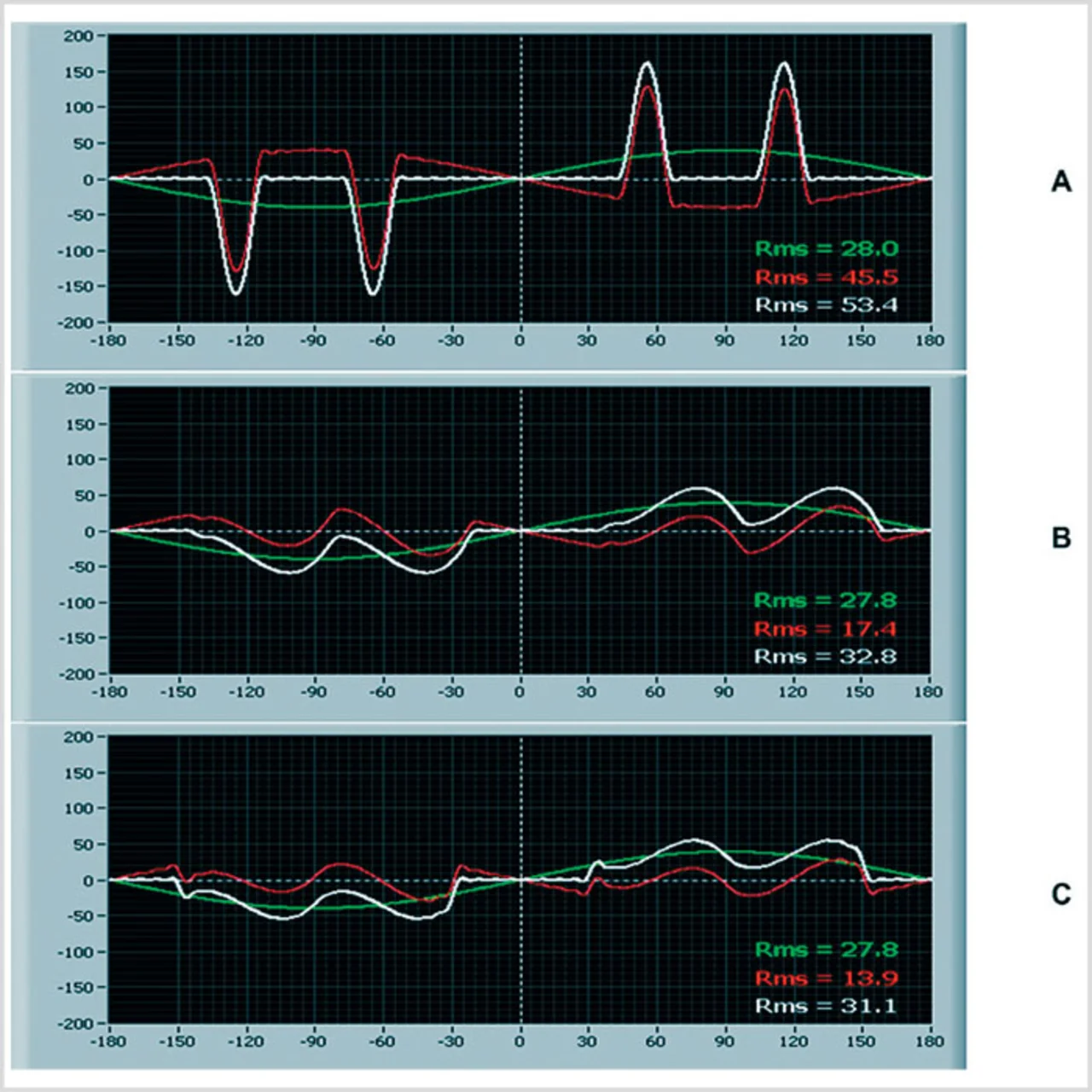
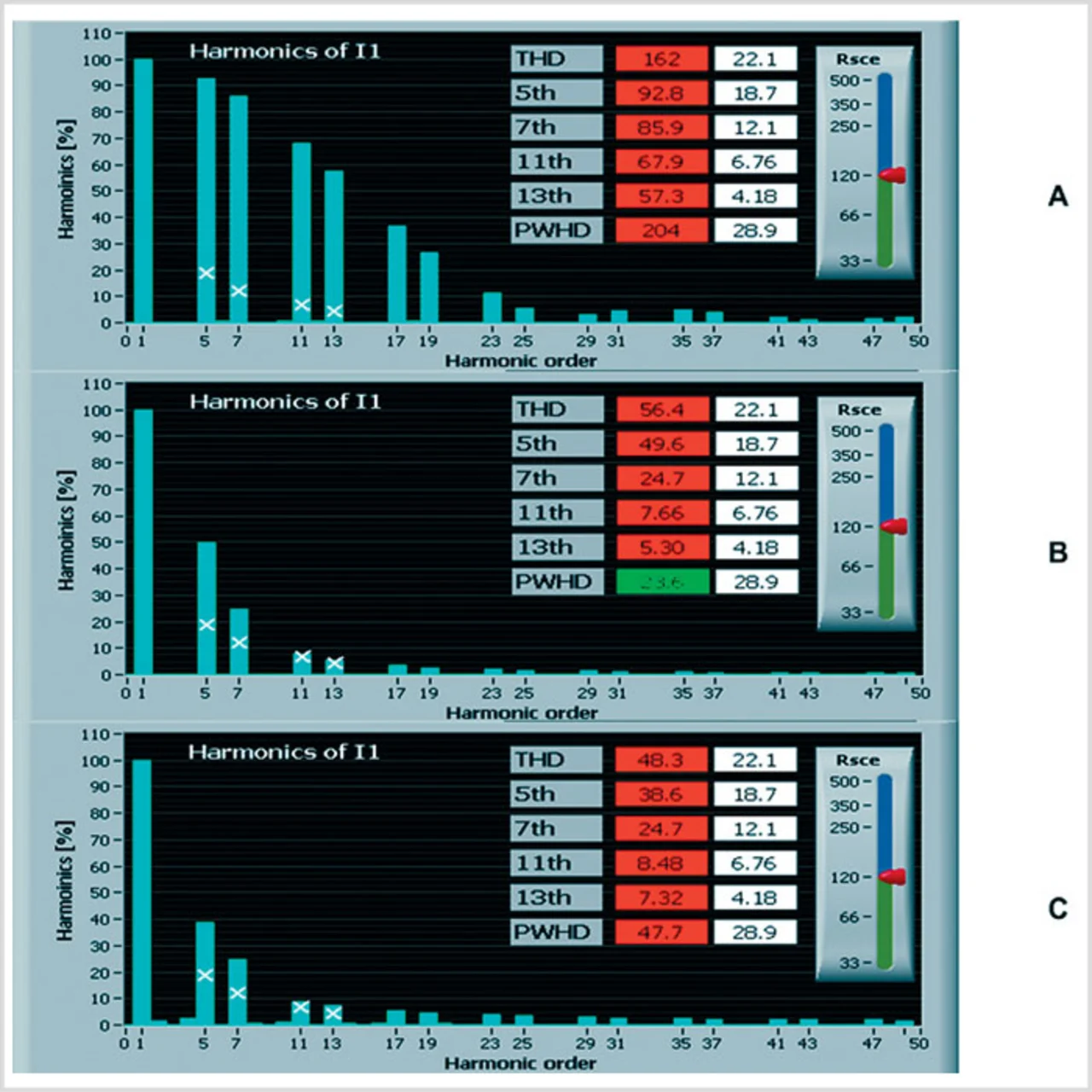
Der reaktive Strom ib (rot) oder Blindstrom ist somit der verbleibende Stromanteil, also die Differenz zwischen der weißen und der grünen Kurve. Dieser reaktive Stromanteil schiebt ausschließlich Blindleistung zwischen der Quelle und der Last hin und her und trägt nichts zur Übertragung von Wirkleistung bei. Das Spektrum des Blindstroms setzt sich aus Oberwellen und reaktiven Anteilen der Grundschwingung zusammen. In den Kurven aus Bild 2 sind die reaktiven Anteile der Grundschwingung jedoch vernachlässigbar. Der Blindstrom ib besteht hauptsächlich aus den ungeradzahligen Oberwellen ab der 5. Ordnung, wobei höherfrequente harmonische Oberwellen (>25. Oberwelle) vernachlässigbar sind.
Der reaktive Stromanteil verursacht Zusatzverluste in der Netzleitung und führt zu nichtsinusförmigen Spannungsabfällen über der Netzimpedanz, die für die Verformung der Netzspannung und somit für schlechte „Power Quality“ verantwortlich sind. Daher lässt sich sagen, dass der Blindstrom kontraproduktiv und somit weitestgehend zu eliminieren ist.
Die Aufteilung von nichtsinusförmigen Strömen (von einer sinusförmigen Spannungsquelle bezogen) in aktive und reaktive Anteile wurde zum ersten Mal 1932 von S. Fryze vorgeschlagen [1]. Die Effektivwerte der Ströme i, ia, ib mit der Bezeichnung I, Ia, Ib können anhand der folgenden Formel in Bezug gebracht werden:

- Reduzierung von Netzoberwellen korrekt berechnen
- Reduzierung von Netzoberwellen korrekt berechnen
- Reduzierung von Netzoberwellen korrekt berechnen
- Korrekte Bemessung passiver Oberwellenfilter
- Reduzierung von Netzoberwellen korrekt berechnen
- Last und Blindstrom sind entscheidend