Schätzen war früher
Ausgangskapazität bei Soft-Switching-Wandlern bestimmen
Beim Design eines Leistungswandlers, der im Spannungsnulldurchgang schaltet, gehört besonders die Ausgangskapazität zu den entscheidenden Parametern. Denn diese bestimmt, welche Induktivität benötigt wird, um die ZVS-Bedingung zu erreichen. Bisher mussten Entwickler mit groben Annahmen für die Ausgangskapazität auskommen. Doch Schätzen war früher.
Um die Leistungsdichte zu maximieren, steigen die Schaltfrequenzen der Schaltwandler stetig. Daher werden auch Soft-Switching-Verfahren wie das Schalten im Spannungsnulldurchgang (ZVS) immer beliebter. Bei höheren Schaltfrequenzen lassen sich die parasitären Effekte von Leistungs-MOSFETs allerdings nicht mehr vernachlässigen. Unter den parasitären Elementen gehört besonders die Ausgangskapazität zu den entscheidenden Parametern beim Design eines Leistungswandlers mit ZVS-Topologie. Diese bestimmt, welche Induktivität benötigt wird, um die ZVS-Bedingung zu erreichen.
Bislang nutzten die Entwickler nur grobe Annahmen, um den richtigen Wert für die Ausgangskapazität mittels der Gleichungen zu ermitteln. Dieser konventionelle Äquivalenzwert für die Ausgangskapazität ist allerdings für reale Anwendungen nicht besonders hilfreich, da dieser von der Drain-Source-Spannung abhängig ist und die bei den Ein-/Aus-Schaltvorgängen gespeicherte Energie nicht genau berücksichtigt wird. Ein neues Konzept zur Ermittlung der Ausgangskapazität, das auch die bei der jeweiligen Arbeitsspannung des Leistungswandlers gespeicherte Energie berücksichtigt, ermöglicht ein optimales Design des Leistungswandlers.
Bei der Soft-Switching-Topologie nutzt man die Energie, die in der Induktivität, dem Leckstrom und der Serieninduktivität oder Magnetisierungsinduktivität des Transformators gespeichert ist, um den Leistungsschalter einzuschalten. Dabei wird die Ausgangskapazität der Schalter durch Resonanz entladen. Um ein hartes Schalten zu vermeiden, das zusätzliche Leistungsverluste verursacht, ist die Induktivität genau zu dimensionieren. Die Gleichungen (1) und (2) formulieren die Grundvoraussetzungen für ein Schalten im Spannungsnulldurchgang. Dabei stehen Ceq für die äquivalente Ausgangskapazität der Schalter, CTR für die parasitäre Kapazität des Transformators sowie CS für die äquivalente Ausgangskapazität der Schalter.


Die Gleichung (1) ist für eine phasenverschobene Vollbrückentopologie und die Gleichung (2) für eine LLC-Resonanz-Halbbrückentopologie zu verwenden. Die Ausgangskapazität spielt in beiden Gleichungen eine wichtige Rolle. Wird eine zu große Ausgangskapazität in Gleichung (1) angenommen, dann ergibt sich eine größere Induktivität. Die große Induktivität reduziert die Stromsteilheit (di/dt) und damit die effektive Nutzleistung des Leistungswandlers. Dagegen hat eine zu kleine Ausgangskapazität eine kleinere Induktivität und deshalb ein unerwünschtes hartes Schalten zur Folge. Auch eine zu große Ausgangskapazität in (2) begrenzt die Magnetisierungsinduktivität und verursacht einen höheren zirkulierenden Strom.
Deswegen ist eine genaue Ermittlung der Ausgangskapazität der Schalter entscheidend, um einen Soft-Switching-Wandler optimal designen zu können. Normalerweise tendiert bei einer konventionellen Annahme die äquivalente Ausgangskapazität eher zu einem größeren Wert. Die Entwickler sollten die Leistungswandler daher nach der Auswahl der Induktivität mittels (1) oder (2) nochmals anpassen. Dies erfordert meist einige Iterationen, da zum Beispiel Windungsverhältnis, Streuinduktivität und das effektive Tastverhältnis voneinander abhängen. Zudem verändert sich die Ausgangskapazität eines Leistungs-MOSFETs auch mit der Drain-Source-Spannung. Eine Ausgangskapazität, die eine äquivalente gespeicherte Energie bei der Arbeitsspannung des Leistungswandlers liefert, ist die beste Alternative für diese Anwendungen.
Gespeicherte Energie in Ausgangskapazität
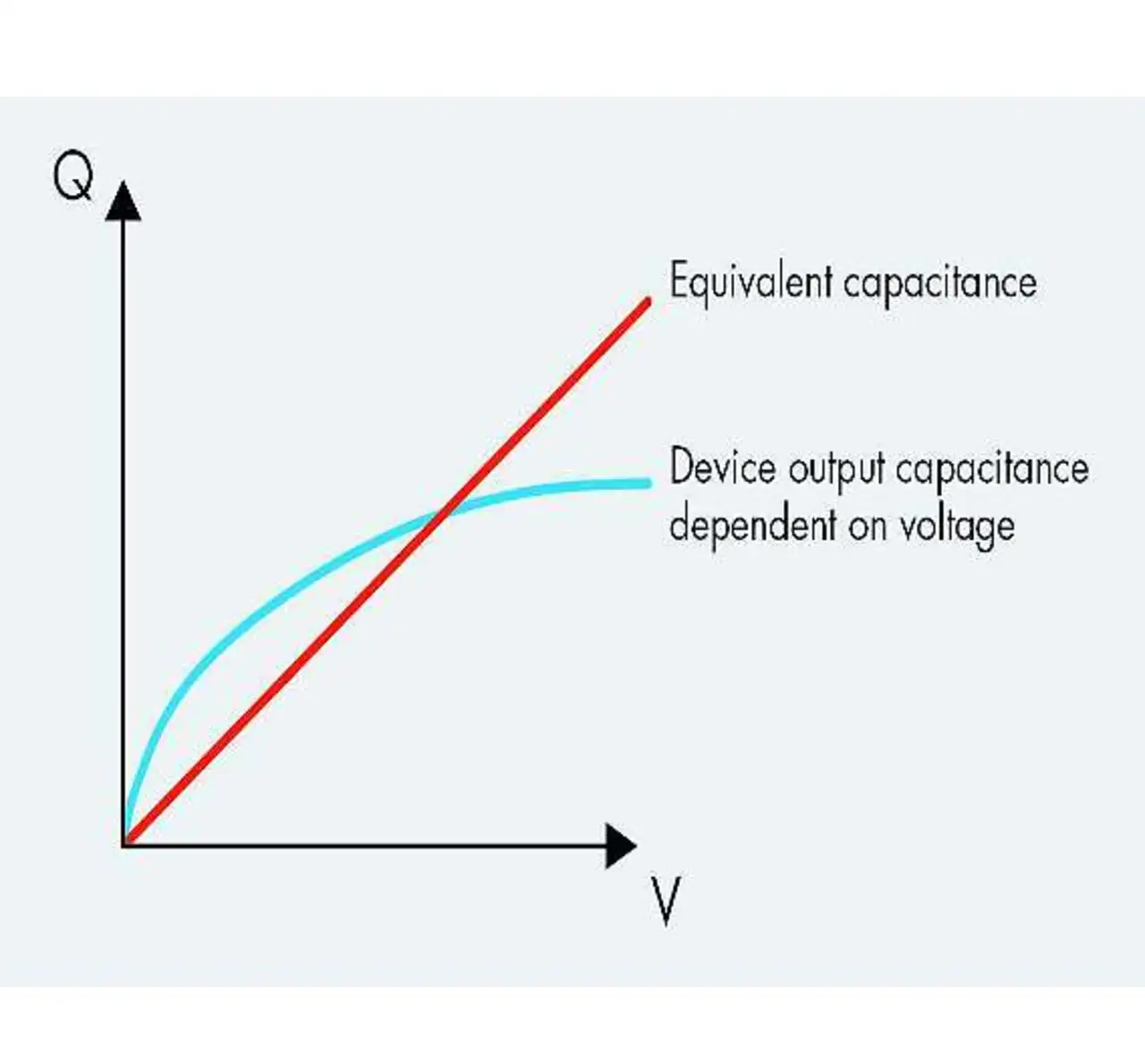
In der Spannungs-Ladungs-Kurve wird die Kapazität durch die Steilheit einer Gerade und die in der Kapazität gespeicherte Energie durch die unter der Linie liegende Fläche dargestellt. Die Ausgangskapazität des Leistungs-MOSFETs ist allerdings nichtlinear und verändert sich je nach Drain-Source-Spannung. Die in der Ausgangskapazität gespeicherte Energie entspricht trotz des nichtlinearen Kapazitätswerts aber immer noch der Fläche unterhalb der Linie. Wird also eine Gerade eingezeichnet, welche die gleiche Fläche abdeckt, wie die Kurve der veränderlichen Ausgangskapazität in Bild 1, dann ergibt sich die äquivalente Ausgangskapazität und somit die gespeicherte Energie über die Steigung der Linie.
Bei MOSFETs, die auf der etwas älteren planaren Technologie basieren, können die Entwickler mit Hilfe einer Kurvenannäherung eine äquivalente Ausgangskapazität auf der Basis der im Datenblatt angegebenen Ausgangskapazität ermitteln. Diese wird normalerweise bei einer Drain-Source-Spannung von 25 V angegeben (Gleichung 3).

Dann lässt sich die gespeicherte Energie mit einer einfachen Integration gemäß Gleichung (4) errechnen.

Schließlich ergibt sich die effektive Ausgangskapazität nach Gleichung (5).

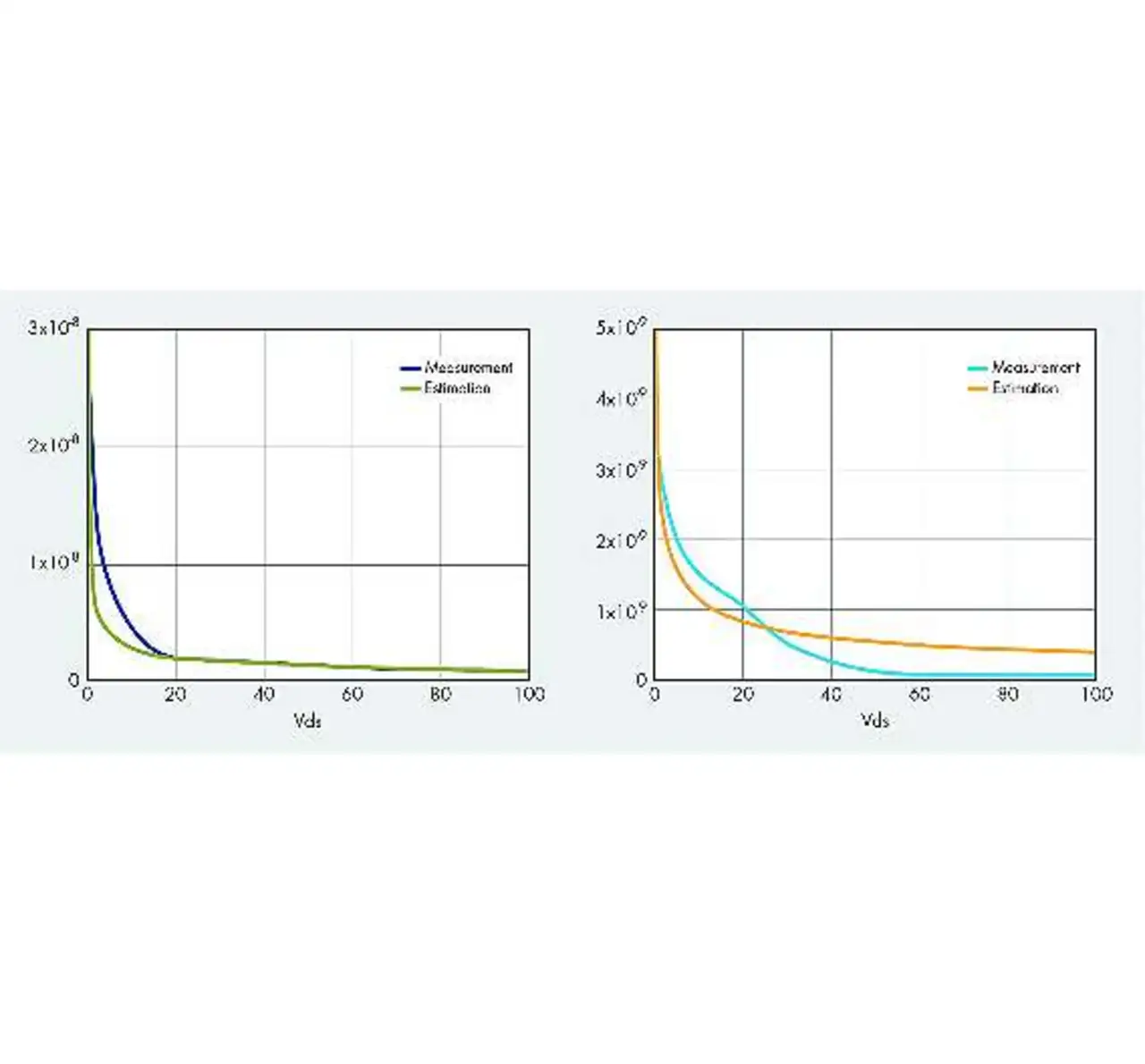
Bild 2 zeigt die Messung der Ausgangskapazität und die dazu passende Kurve der Gleichung (3). Dies ist bei MOSFETs auf der Basis der alten planaren Technologie kein Problem (Bild 2, links). Auf der neuen Technologie basierende MOSFETs wie Super-Junction haben eine stärker nichtlineare Ausgangskapazität, sodass eine einfache Exponentialkurve nicht immer passt.
Bild 2 zeigt rechts die Messwerte der Ausgangskapazität eines MOSFETs mit neuester Technologie und die passende Kurve mit Gleichung (3). Bei höheren Spannungen ergibt sich eine große Differenz, da die Spannung während der Integration mit der Kapazität multipliziert wird.
Die Abschätzung in Bild 2 (rechts) ergibt einen viel größeren äquivalenten Kapazitätswert, der beim Design des Wandlers anfangs in die Irre führen kann.
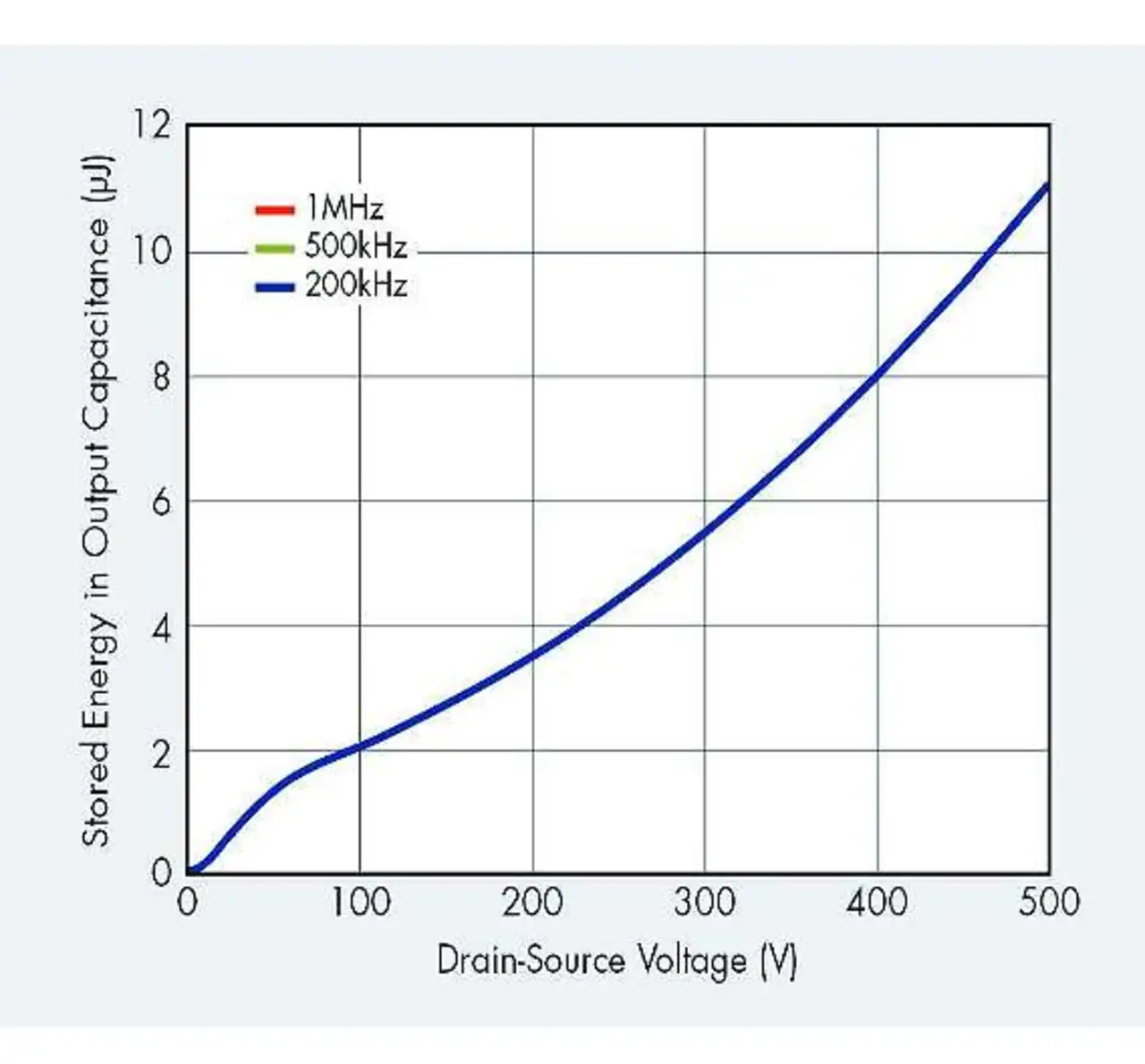
Wenn die Werte der Ausgangskapazität für die verschiedenen Drain-Source-Spannungen verfügbar sind, dann lässt sich die in der Ausgangskapazität gespeicherte Energie mittels Gleichung (4) errechnen.
Zwar ist die Kapazitätskurve im Datenblatt dargestellt, trotzdem ist ein genaues Auslesen des Kapazitätswerts aus dem Diagramm nicht einfach. Daher wird die in der Ausgangskapazität gespeicherte Energie in Abhängigkeit von der Drain-Source-Spannung bei den neuesten Leistungs-MOSFETs in einem Diagramm im Datenblatt dargestellt.
Mit der in Bild 3 gezeigten Kurve lässt sich die äquivalente Ausgangskapazität bei einer bestimmten Spannung dann mittels Gleichung (5) errechnen.
Fragen zur Ausgangskapazität
Da Leistungs-MOSFETs üblicherweise bei erhöhter Temperatur betrieben werden, ergeben sich während der Entwicklung von Schaltnetzteilen oftmals Fragen zum Temperaturkoeffizienten der MOSFET-Kapazität. Die MOSFET-Kapazität kann man prinzipiell als konstant über die Temperatur ansehen.
Der MOSFET-Kapazitätswert ist von der Verarmungslänge, Dotierungskonzentration, Kanalbreite und Dielektrizitätskonstante des Halbleiters abhängig, die sich aber alle kaum über die Temperatur verändern. Auch die Schalteigenschaften des MOSFETs, wie die Schaltverluste oder die Ein-/Aus-Übergangsgeschwindigkeit, ändern sich nicht mit der Temperatur, da das Bauteil über Majoritätsladungsträger funktioniert und somit die Schaltzeit hauptsächlich durch den Kapazitätswert bestimmt wird.
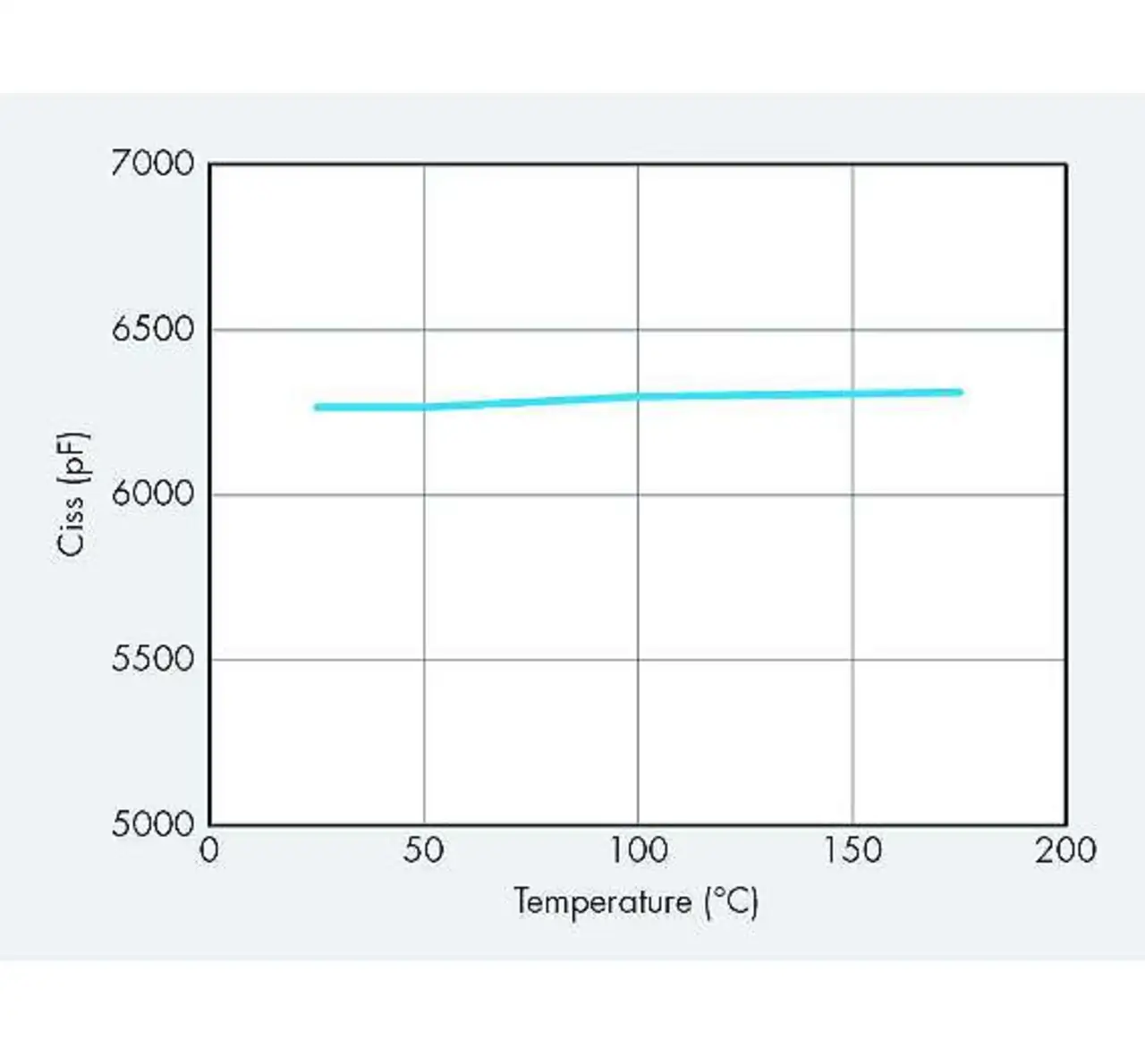
Der äquivalente Serienwiderstand am Gate steigt mit zunehmender Temperatur etwas an. Dies kann das Schaltverhalten des MOSFETs bei höheren Temperaturen etwas verlangsamen. Bild 4 zeigt die Veränderung des Kapazitätswerts mit der Temperatur. Die Änderung liegt bei weniger als 1% über einen Temperaturbereich von etwa +25 °C bis +175 °C.
Ein weiterer für die Entwickler interessanter Bereich sind die Testbedingungen für die MOSFET-Kapazität. In den meisten Fällen wird die Ausgangskapazität mit einer Frequenz von 1 MHz und einer Gate-Source-Spannung VGS von 0 V gemessen. Es gibt Kapazitätswerte zwischen Gate und Drain, zwischen Gate und Source sowie zwischen Drain und Source. In der Praxis ist allerdings die separate Messung der einzelnen Kapazitätswerte nicht möglich. Deswegen wird die Summe des Gate-Drain-Kapazitätswerts und des Drain-Source-Kapazitätswerts als Ausgangskapazität bezeichnet, und die Messung erfolgt durch die Parallelschaltung der beiden Kapazitätswerte. Um diese Parallelschaltung zu erreichen, werden Gate und Source kurzgeschlossen, daher gilt VGS = 0 V.
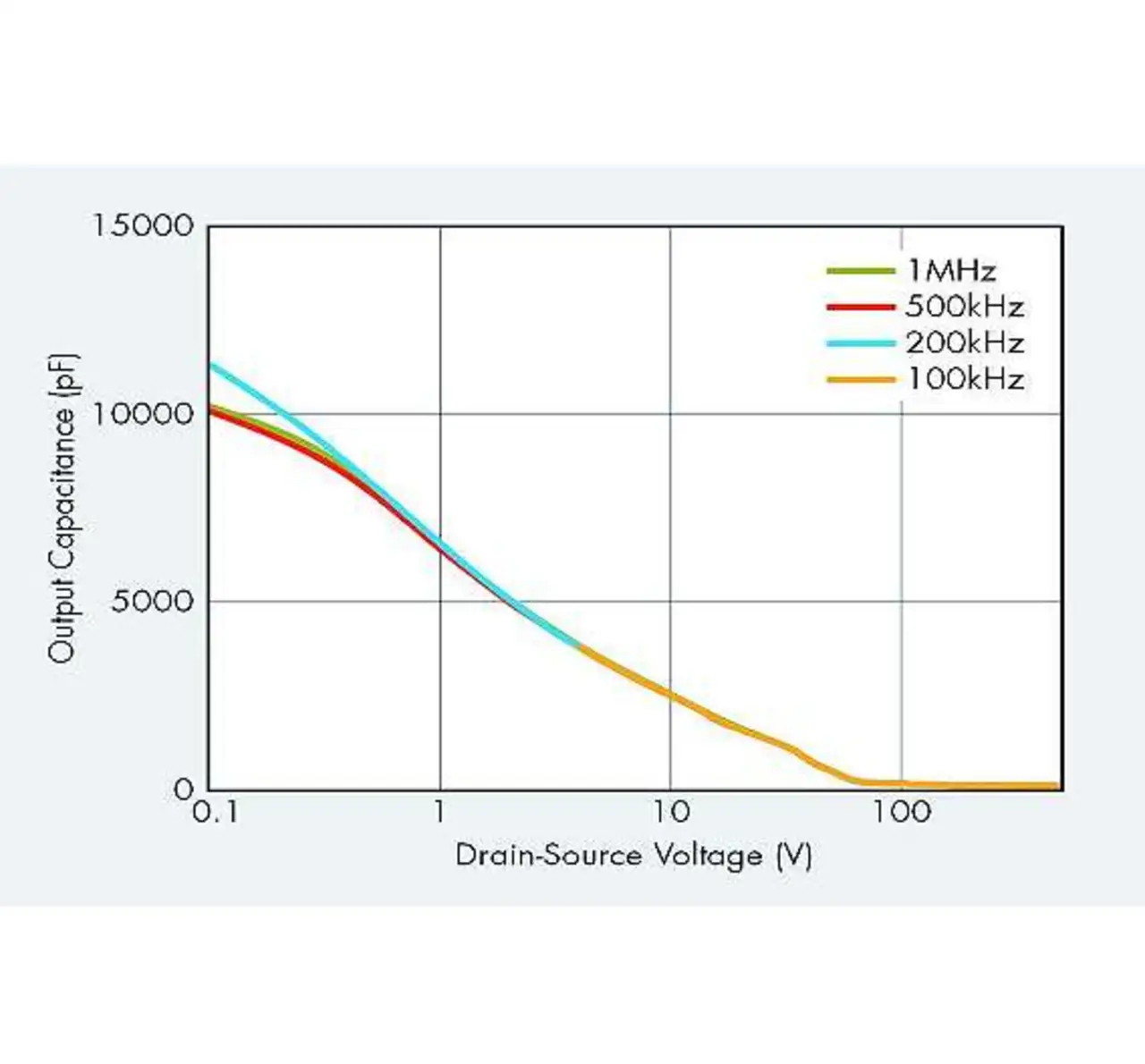
In Schaltanwendungen ist die Ausgangskapazität durch den MOSFET-Kanal kurzgeschlossen, wenn das Bauteil mittels einer Gate-Vorspannung eingeschaltet ist. Nur wenn der MOSFET ausgeschaltet ist, sollte die Ausgangskapazität berücksichtigt werden. Der Kapazitätswert steigt etwas bei niedriger Frequenz und kleiner Spannung (Bild 5). Bei niedriger Frequenz ist der Kapazitätswert bei einer kleinen Drain-Source-Spannung aufgrund von Einschränkungen der Messinstrumente manchmal nicht messbar.
In Bild 5 ist die Kapazität bei 100 kHz nicht messbar, wenn die Drain-Source-Spannung kleiner als 4 V ist. Obwohl sich die Ausgangskapazität nur wenig ändert, ist die äquivalente Ausgangs-kapazität fast konstant, da sich eine geringe Änderung der Ausgangskapazität bei einer kleinen Spannung kaum auf die gespeicherte Energie auswirkt (Bild 3). Der äquivalente Wert der Ausgangskapazität sollte also eher als Einzelwert bei einer festen Drain-Source-Spannung berücksichtigt werden. Die Versuchsbedingungen und Temperaturkoeffizienten sind dabei zu beachten.
Über den Autor:
Sungmo Young ist Application Engineer im Bereich Power Supply System bei Fairchild Semiconductors.




