Startseite > Messen + Testen > Wie spät ist es genau?

Regelalgorithmen für IEEE-1588

Wie spät ist es genau?

26. September 2017, 8:00 Uhr | Von Peter Plazotta, TSEP

▶ Diesen Artikel anhören

Fortsetzung des Artikels von Teil 5

Der Kalman-Filter

Bereits 1960 entwickelte Rudolf E. Kalman für zeitdiskrete lineare Systeme ein spezielles Verfahren, um aus verrauschten und teilweise redundanten Messungen die Zustände eines Systems (inklusive deren Parameter) zu schätzen. Dieses Verfahren wurde als Kalman-Filter bekannt und erstmals in [3] veröffentlicht. Seither sind viele verschiedene Varianten des Kalman-Filters veröffentlicht worden. Eine detailierte Beschreibung kann in [5] nachgelesen werden.

Damit der Kalman-Filter richtig eingesetzt werden kann, ist es notwendig, dass die Grundbedingungen des Messsystems bekannt sind. Jeder klassische Kalman-Filter besteht in der Regel aus einer Zustandsraumbeschreibung und dem realen Messsystems mit dem ihm eigenen System- und Messrauschen.

Jobangebote+ passend zum Thema

Ingenieur/Elektroingenieur/Elektrotechniker als Field Application Engineer

GEYER Electronic GmbH, Planegg

Alle Jobangebote im Elektroniknet Karrierebereich anzeigen

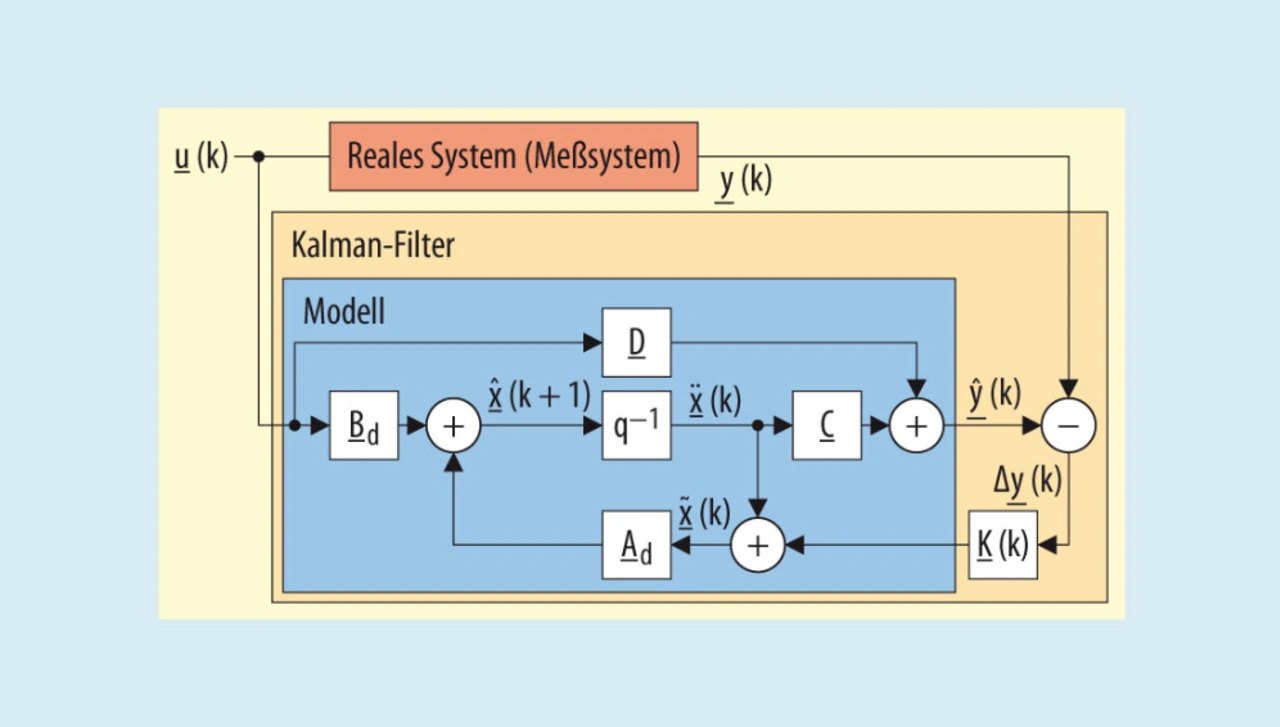
Grundsätzlich schätzt ein Kalman-Filter die Ausgangsgröße ŷ(k) und vergleicht diese mit der gemessenen realen Ausgangsgröße y(k). Die Differenz Δy(k) der beiden Werte wird zur Korrektur des geschätzten Zustandsvektors ¨x(k) verwendet. Die Struktur lässt sich wie in Bild 6 beschreiben.

Beim Entwurf eines Kalman-Filters ist es notwendig, das physikalische System mit Hilfe von Differenzialgleichungen zeitkontinuierlich zu beschreiben. Bei der Bestimmung der Zustandsvariablen kann es mehrere Ansätze geben. In der Regel sollten diese Möglichkeiten evaluiert werden und der Ansatz, der das Problem an besten beschreibt, sollte dann verwendet werden.

Wenn man die einzelnen Schritte betrachtet, die zu einer vollständigen Beschreibung des Zustandsraumes führen, kann man sagen, dass die Erstellung eines Kalman-Filters alles andere als trivial ist. Jedoch können die Randbedingungen des Messsystems optimal in den Kalman-Filter eingebettet werden, was zu einer bestmöglichen Korrektur der internen IEEE-1588-Uhr führt.

Analyse im Vorfeld

Der erfolgreiche Einsatz einer IEEE-1588-Implementierung basiert nicht nur auf der Verwendung eines bestehenden IEEE-1588-Stacks oder einer speziellen Hardware. Der problemorientierte Lösungsansatz ist hier der Schlüssel zum Erfolg. Die Möglichkeiten von IEEE 1588 sind breit gefächert. Ohne jedoch die Anforderungen an die notwendige Genauigkeit und die zur Verfügung stehende Hardware-Topologie zu kennen, ist es nur schwer möglich, ein funktionierendes System bereitzustellen. Die Analyse im Vorfeld ist zwingend notwendig und erfordert ein entsprechendes Know-how.

Der Artikel erhebt nicht den Anspruch, alle Facetten an dieser überaus komplexen Materie darzustellen, sondern soll einen kleinen Überblick geben, welche Probleme und Lösungsansätze vorhanden sind. Jeder verfügbare IEEE-1588-Stack stellt nur das Handwerkszeug für eine Umsetzung dar. Die richtige Verwendung und die Umsetzung des Regelalgorithmus ist die eigentliche Aufgabe.

Literatur

Improving IEEE 1588 synchronization accuracy in 1000BASE-T systems, Rodney Greenstreet and Alejandro Zepeda.
White Rabbit Project. White rabbit wiki, 2016.
Kalman, R. E.: A New Approach to Linear Filtering and Prediction Problems (Transaction of the ASME, Journal of Basic Engineering). 1960, S. 35–45.
Accurate Time Synchronization in PTP-based Industrial Networks with Long Linear Path, Daniele Fontanelli and David Macii.
R. Marchthaler, S. Dingler: Kalman-Filter, Springer Vieweg.

Der Autor

Dipl. Ing (FH) Peter Plazotta ist CEO von TSEP und seit 30 Jahren mit dem Design und der Entwicklung von Systemsoftware vor allem in den Bereichen T&M, Telekommunikation und Automotive beschäftigt. Er widmet sich seit über zehn Jahren dem Thema IEEE 1588 und hat in diesem Bereich mehrere Implementierungen mit seiner Firma begleitet.