Sparhilfe oder Schlangenöl?
Leistungsfaktorkorrektur – Eine Einführung
Eine neue Masche haben die »Schlangenölverkäufer« in den USA aufgetan: »Power Saver«, die, mit dem Stromnetz verbunden, Energie sparen beziehungsweise die Stromrechnung senken sollen. Dabei handelt es sich um Geräte zur Leistungsfaktorkorrektur, welche die vom Stromzähler gemessene Scheinleistung verbessern sollen. Nun wird die Stromrechnung für Privathaushalte natürlich nach Wirkleistung und nicht nach Scheinleistung abgerechnet, sodass sie kaum sinken wird. Das sieht in Industrieanwendungen etwas anders aus.
Zu Beginn ist es sinnvoll, einige Grundlagen darzustellen. Immerhin geschieht es selbst Profis, dass sie Leistungswerte in Watt (W) und Volt-Ampere (VA) miteinander verwechseln. Die Momentanleistung (auch Augenblicksleistung) ist definiert als p(t) = u(t) x i(t), wobei u(t) die Momentanspannung zur Zeit t und i (t) der Momentanstrom zur Zeit t sind.
Für eine einfache Wechselstromschaltung definiert sich die Wirkleistung als arithmetischer Mittelwert der Momentanleistung über eine volle Periodendauer, also Wirkleistung = Mittelwert {u(t) x i(t)}.
Diese wird in Watt angegeben und steht für die von einem elektrischen Strom verrichtete reale Arbeit beziehungsweise die von einer Last verbrauchte reale Energie. Liegt eine sinusförmige Spannungsquelle an einem Widerstand an, so fließt ein ebenfalls sinusförmiger Strom, und die Leistung setzt der Widerstand in Wärme um.
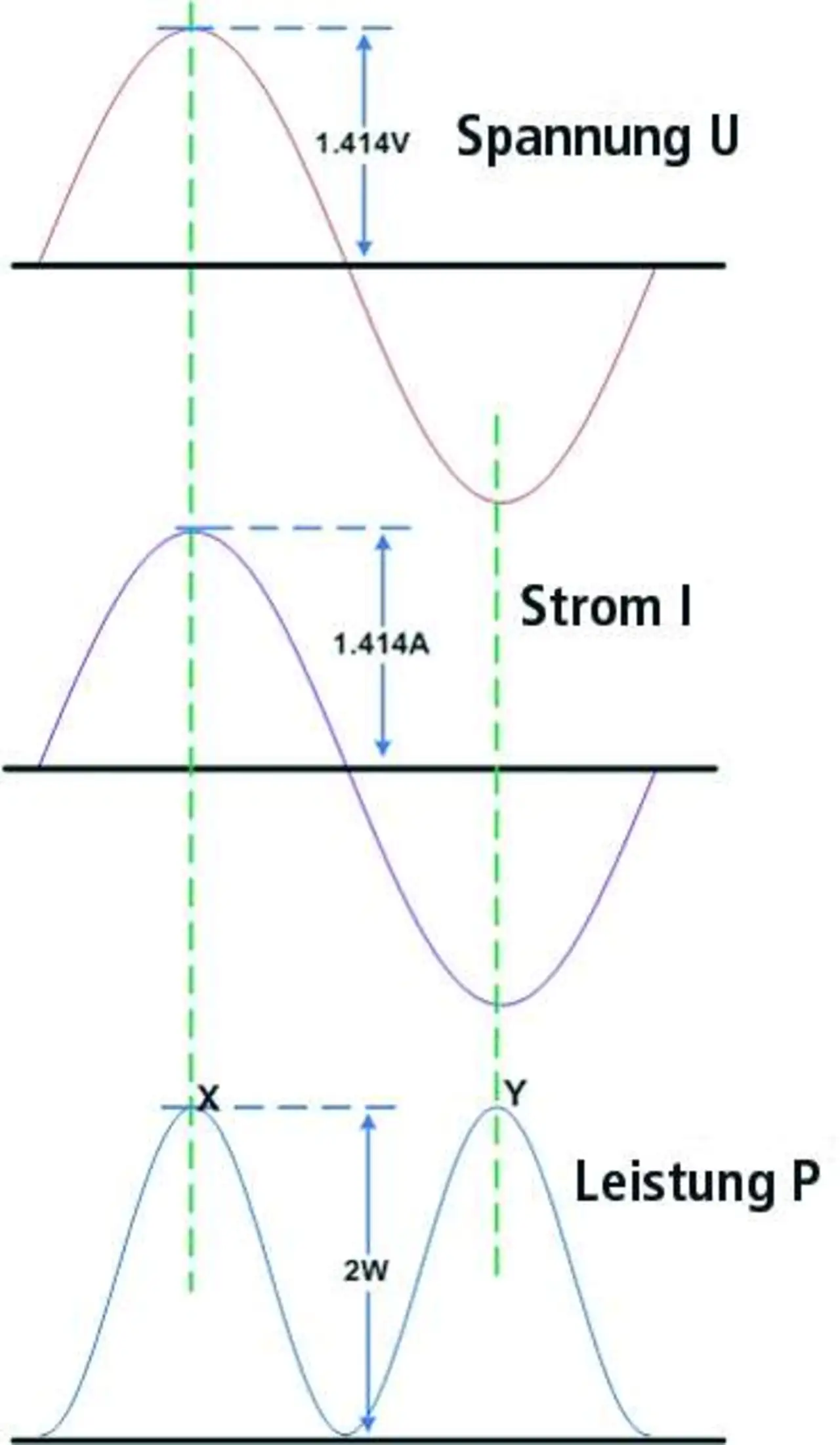
Bild 1 zeigt die Momentanleistung als Produkt von Spannung und Strom mit den Werten Ueff = Effektivwert der Spannung = 1 V, Uss = Spitzenspannung = 1,414 V, Ieff = Effektivwert des Stroms = 1 A, Iss = Spitzenwert des Stroms = 1,414 A und R = 1 Ω.
Die Werte verändern sich über die Zeit.
Die Momentanleistung an den Spitzenwerten von Spannung und Strom (Punkt »X« in Bild 1) beträgt 1,414 V x 1,414 A = 2 W (im Modell dient der Wert 1,414 als Näherung für √2, eine irrationale Zahl).
Auf gleiche Weise berechnet sich die Momentanleistung beim Maximum von negativer Spannung und negativem Strom (Punkt »Y« in Bild 1) zu -1,414 V x -1,414 A = 2 W. Die Durchschnittsleistung während der Sinusperiode liegt bei 1 W.
Reaktanzen
Elektrische Systeme kommen meist nicht ohne Induktivitäten und Kapazitäten aus, auch Reaktanzen genannt.
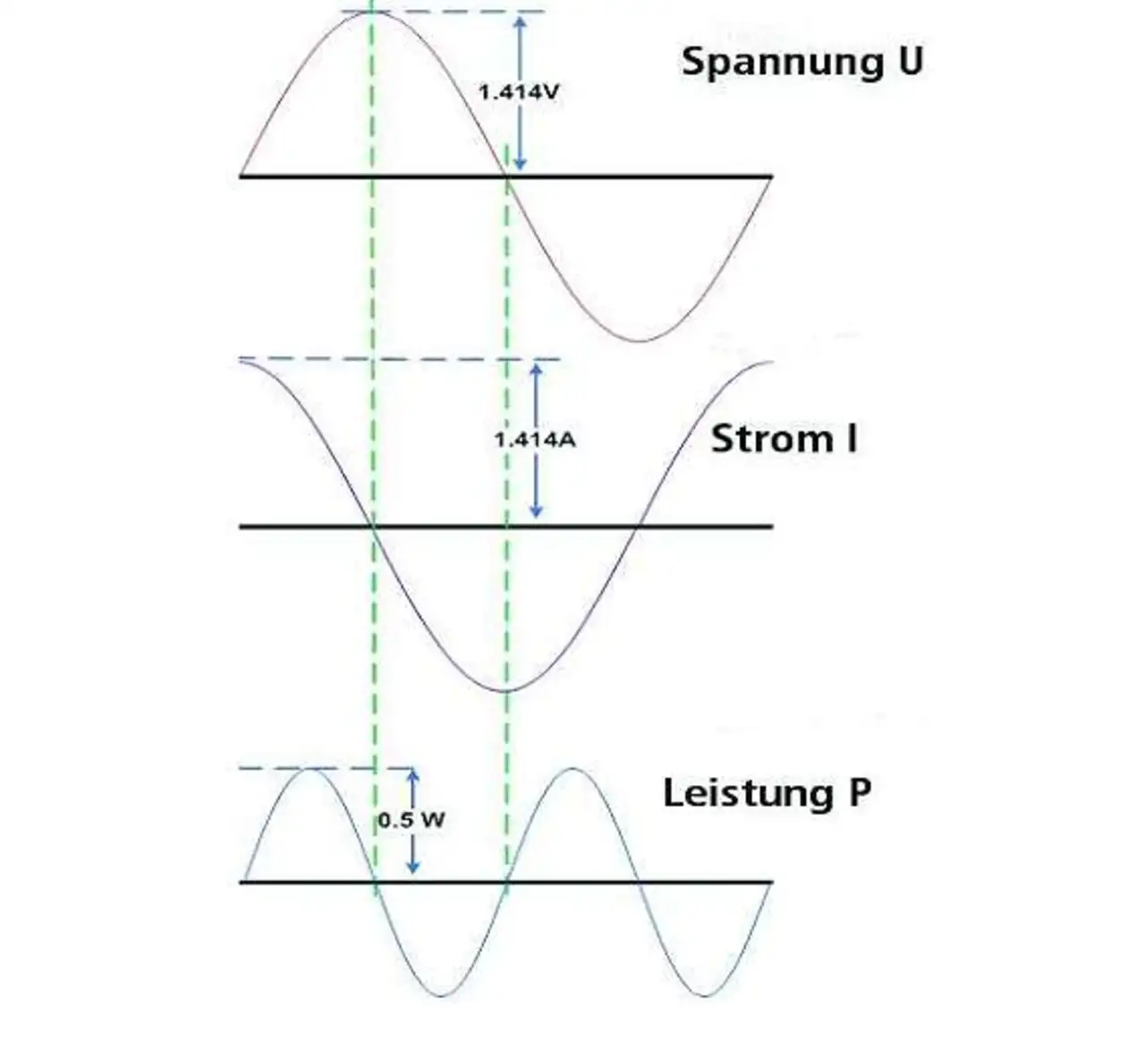
Bei gleicher induktiver Last würde der Strom in einer idealen Induktivität gegenüber der angelegten Spannung exakt 90° nachlaufen, wie in Bild 2 dargestellt.
Zwischen den zwei im Diagramm eingezeichneten vertikalen Linien ergibt der negative Strom multipliziert mit der positiven Spannung eine negative Leistung. Die für einen Teil der Periodendauer auftretende negative Leistung würde bedeuten, dass unter dem Strich Energie von der Induktivität (Last) zurück in die Energiequelle gespeist würde.
Ideale Reaktanzen (bei ihnen beträgt der Phasenunterschied zwischen Strom und Spannung exakt 90°) verbrauchen demzufolge keine Energie, aber sie lassen trotzdem Ströme fließen und erzeugen Spannungsabfälle. Diese »imaginäre Leistung« ist die Blindleistung.
Der über eine volle Periodendauer des Sinussignals gemessene Mittelwert beläuft sich wegen der Phasenverschiebung zwischen Spannung und Strom auf Null, das heißt, er trägt nicht zu einem Netto-Energietransfer bei (wie in Bild 2 gezeigt). Die Blindleistung wird in Volt-Ampere-Reaktiv (VAr) angegeben.
Die Kombination von Wirk- und Blindleistung ergibt die Scheinleistung (oder Gesamtleistung) in Volt-Ampere (VA).
Der Leistungsfaktor
Der Leistungsfaktor l ist definiert als Verhältnis von Wirkleistung zur Scheinleistung. Im Allgemeinen ist also W ungleich VA, es sei denn, der Leistungsfaktor eines Verbrauchers wäre 1.
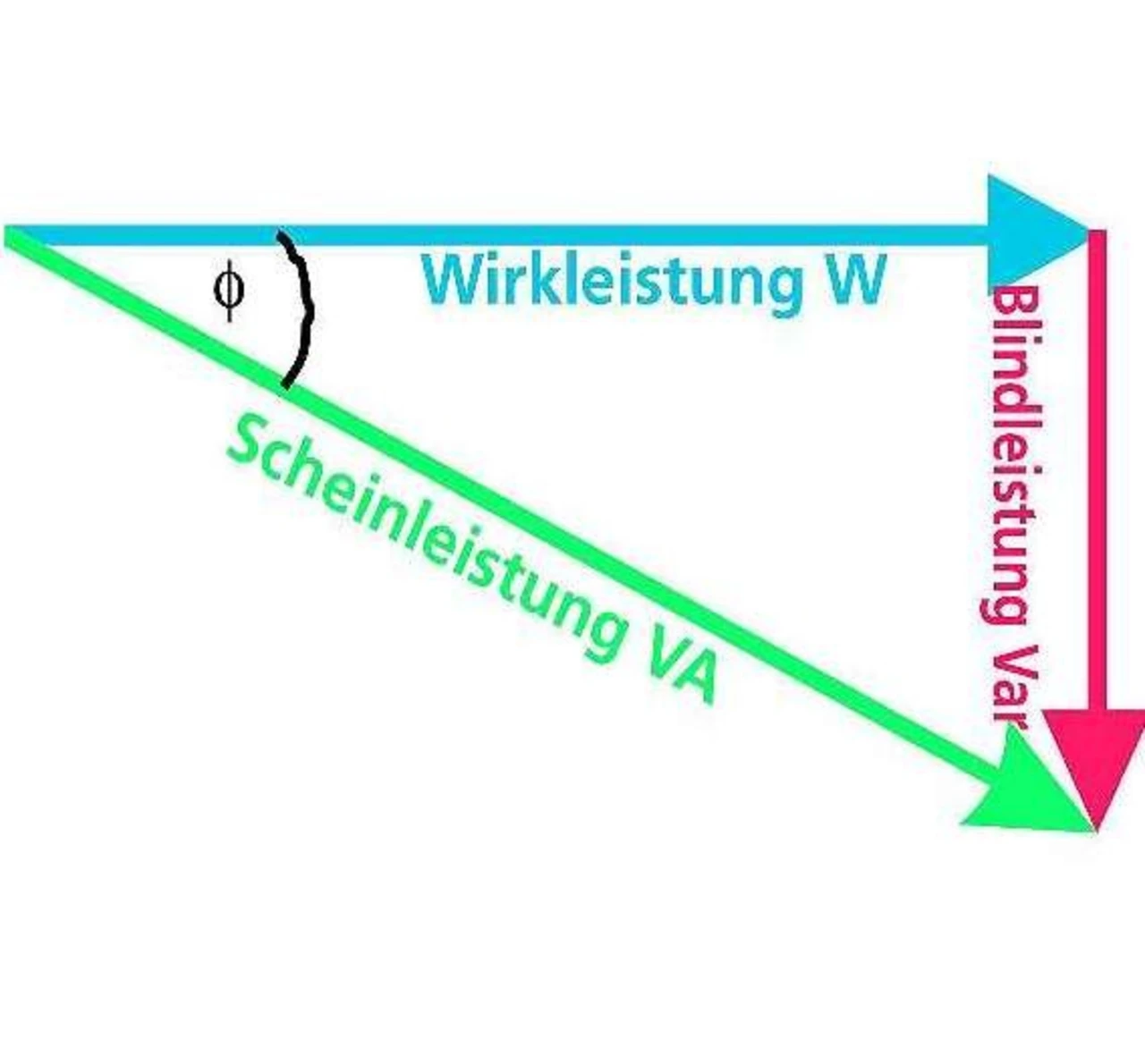
Bild 3 zeigt das Leistungsdreieck, in dem die Beziehungen zwischen Wirkleistung, Blindleistung und Scheinleistung als Vektordiagramm dargestellt sind.
Man beachte, dass für den Fall sinusförmiger Spannungen und Ströme l = cos(ϕ) beträgt, mit ϕ als Phasenwinkel zwischen Spannung und Strom. Im Falle einer rein resistiven Schaltung, beispielsweise einer Glühbirne, beträgt der Leistungsfaktor 1, da die Blindleistung bei Null liegt.
Dann würde das Leistungsdreieck wie eine horizontale Linie aussehen, da die Höhe (Blindleistung) auf Null schrumpft. Für eine rein induktive Schaltung beträgt der Leistungsfaktor Null, weil die Wirkleistung bei Null liegt.
In diesem Falle würde das Leistungsdreieck wie eine vertikale Linie aussehen, da die Grundlinie (Wirkleistung) auf Null schrumpft. Das Gleiche gilt sinngemäß für eine rein kapazitive Schaltung. Gibt es keine resistiven Komponenten in der Schaltung, dann muss die Gesamtleistung Null betragen, alle Leistungskomponenten der Schaltung sind dann rein reaktiv.
Auch das Leistungsdreieck für eine rein kapazitive Schaltung wäre eine vertikale Linie (die allerdings in die entgegengesetzte Richtung derjenigen für eine rein induktive Schaltung weist).
In einer Wechselstromschaltung kann der Leistungsfaktor durchaus eine wichtige Rolle spielen, denn jeder Leistungsfaktor kleiner 1 bedeutet, dass die Verdrahtung der Schaltung mehr Strom bewältigen muss, als dies bei Blindleistung Null erforderlich wäre, um eine resistive Last mit gleicher Wirkleistung zu versorgen.
- Leistungsfaktorkorrektur – Eine Einführung
- Leistungsfaktorkorrektur – Eine Einführung
- Leistungsfaktorkorrektur – Eine Einführung