Noise Floor Extension: bei Signal- und Spektrumanalysatoren den Dynamikbereich vergrößern
Das Rauschen (fast) abschaffen
Fortsetzung des Artikels von Teil 2
Das Rauschen (fast) abschaffen
Vorteile der Rauschverminderung bei verschiedenen Signaltypen
CW-Signale: Mäßige Verbesserung
Wie in Bild 2 zu sehen ist, werden Messwertänderungen massiv vervielfacht, wenn man Signale unterhalb des unkompensierten Grundrauschens Pobs N untersucht. Für eine Reduktion des Grundrauschens um 5 dB muss man die Mittelung zehnmal so lang laufen lassen, wenn man die gleiche Standardabweichung (in dB) erreichen möchte wie ohne NFE. Bei einer gewobbelten Analyse bekommt man vergleichbare Ergebnisse: Verringert man die Auflösungsbandbreite um den Faktor Wurzel 10, bekommt man auch eine Verringerung des Grundrauschens von 5 dB und braucht gleichermaßen zehnmal so lange für einen Messdurchgang. Bei CW-Signalen (Continuous Wave) bringt NFE somit lediglich das, was eine Verringerung der Auflösungsbandbreite ebenfalls bringen würde.
Jobangebote+ passend zum Thema
Dieser Vergleich ist allerdings nicht ganz fair, denn es gibt keine perfekten CW. Wenn das Signal noch Reste von FM enthält, kann die Auflösungsbandbreite nicht allzusehr verringert werden, ohne dass die Rest-FM eine Amplitudenungenauigkeit verursacht. Und wenn das Signal Reste von AM enthält, ist zu deren Entfernung ohnehin eine Mittelung sinnvoll. Also kann man auch gleich eine NFE-Kompensation durchführen und von der Verbesserung der Messgenauigkeit profitieren, die diese mit sich bringt.
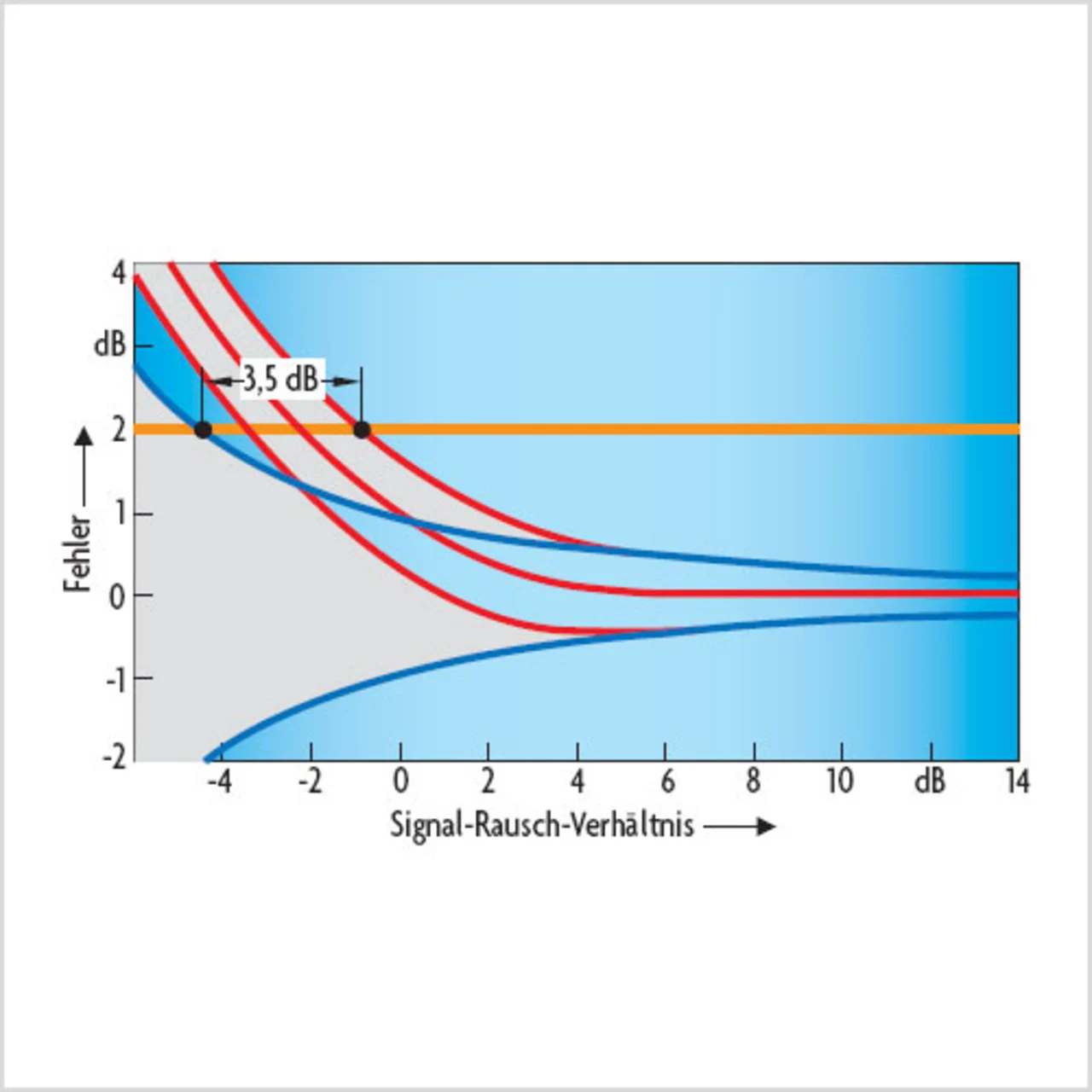
Bild 3 zeigt die Wirkung von NFE auf das 95-%-Intervall der Amplitudengenauigkeit bei Mittelung über viele Messwerte. Bei Messungen ohne NFE setzt man logarithmische Mittelung ein, weil sie den mittleren Fehler bei der Messung von Dauerstrichsignalen bei Überlagerung von Rauschen verringert. Mit NFE setzt man lineare Mittelwertbildung ein, weil der mittlere Fehler mit NFE 0 ist und die Mittelwertbildung eine geringere Varianz ergibt. Man kann erkennen, dass der Signalpegel, den man mit einer Unsicherheit von ±2 dB messen kann, mit NFE um etwa 3,5 dB tiefer liegt als ohne. Bildet man den Mittelwert über noch mehr Messwerte, ist die Verbesserung noch größer. Am Ende des Artikels ist hierfür ein extremes Beispiel angegeben.
Rauschähnliche Signale: dramatische Verbesserungen
NFE funktioniert sehr gut bei rauschähnlichen Signalen wie etwa digitalen Kommunikationssignalen. Für solche Signale braucht man bereits ein nennenswertes Maß an Mittelwertbildung, um die Varianz des Ergebnisses zu reduzieren. Bild 4 zeigt, wie gut das funktionieren kann. Man sieht, dass das Eingangssignal mit NFE mehr als 9 dB schwächer sein kann, und das 95-%-Intervall dennoch innerhalb einer Toleranz von ±1 dB bleibt. (Diese Abbildung basiert auf einer Genauigkeit der 95-%-Perzentile des NFE-Modells, die ausreicht, um den Rauschpegel um 8 dB zu verringern. Dies ist eine konservative Schätzung der Performance im niedrigen Band.)
- Das Rauschen (fast) abschaffen
- Das Rauschen (fast) abschaffen
- Das Rauschen (fast) abschaffen
- Das Rauschen (fast) abschaffen